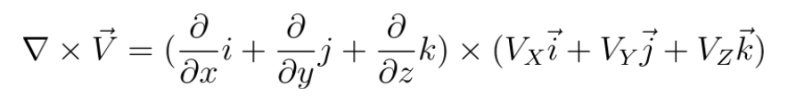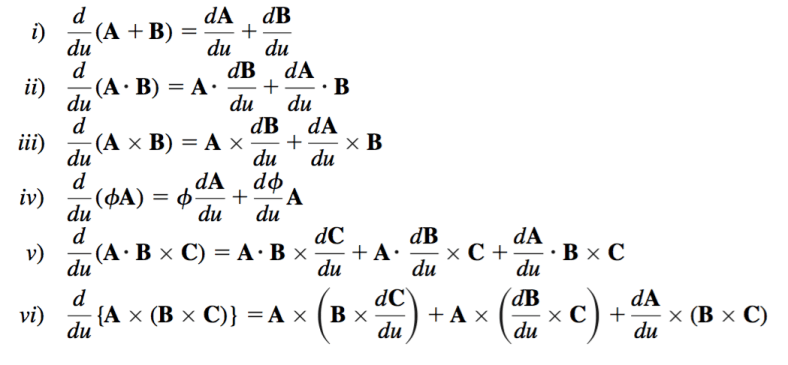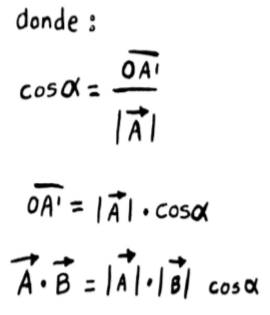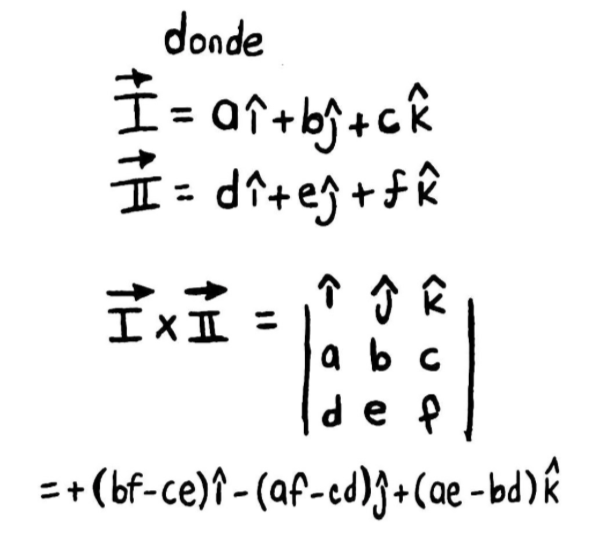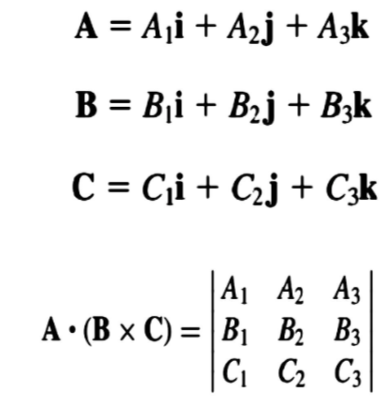Autor Oscar Rosas

Rotacional ∇ × V: De Vector a Vector

Oscar Rosas Deja un comentario

Antes que todo volvamos a definir otro campo vectorial bien bonito (en este caso que sea diferenciable en todos los puntos):

funcion-vectorial

Entonces, el rotacional  se denota se define como :

rotacional-mini

Del mismo modo también se puede expresar en la forma de un determinante:
rotacional-formula

El concepto de rotacional es similar al de divergencia en el sentido de que proporciona información acerca del campo vectorial, pero se trata de una información diferente y algo más difícil de visualizar.

Dicho fatal, ∇× V nos da una idea de la turbulencia del agua en ese punto; dicho un poco menos mal, indica hacia dónde y cómo de rápido giraría una pelota sumergida en ese punto de la bañera.

rotacional 2.png

∇ × V = 0 Quiere decir que no gira la pelota hipotética.

Esto es conocido como un campo irrotacional, y que un campo cumpla esta condición lo convierte en un campo conservativo.

Si ponemos la pelota en cualquier punto de la región izquierda, pasará lo mismo de antes, y si la ponemos en la región derecha, pero ¿qué pasa si la ponemos justo en el borde entre ambos flujos de agua? ¡Ah, ahí la cosa cambia!

rotacional.png

La pelota recibe agua en un sentido por su izquierda, y agua en sentido contrario por su derecha, de modo que –si no es absolutamente lisa, y en nuestra analogía no lo es porque lo digo yo– la pelota girará. En esa línea de frontera entre ambas regiones, el rotacional no es cero. De modo que aquí sí, podemos decir si gira mucho o poco y hacia dónde.

btn1 btn
btn

Divergencia ∇ ·V: De Vector a escalar

Oscar Rosas Deja un comentario

Antes que todo definamos un campo vectorial bien bonito (en este caso que sea diferenciable en todos los puntos)

funcion-vectorial

Ahora sí, las preguntas de siempre:

  • ¿A qué «cosa» puedo sacarle la divergencia? A una función vectorial. 
  • ¿Qué significa sacar la divergencia? Es una operación en la que tu obtienes un escalar (un número pues) iniciando con una función vectorial.
  • ¿Cómo? Así.

divergencia.png

Y si, así de fácil es sacar la divergencia, ¿ves que no son más que unas cuantas formulitas?

Aquí un ejemplo:

Gradiente

¿Qué significa el resultado de esta operación?

La divergencia de un campo vectorial cualquiera, nos dice dónde “nacen” y “mueren” las líneas de campo y cómo de intenso es el proceso de “nacimiento” o “muerte” de las líneas.

Imaginemos nuestro campo vectorial como una bañera, y los vectores como las dirección en la que se mueve el agua, con esta pequeña analogía podemos llegar muy lejos, pues:

Al calcular la divergencia como al calcular la de cualquier vector, sólo pueden pasar una de tres cosas:

  • Si ∇ · V = 0, eso significa que ninguna línea de campo «muere» en el entorno de este punto y ninguna línea de campo «nace». Dicho de otro modo, toda línea que entra en el entorno de este punto sale otra vez de él, y toda línea que sale de aquí entró antes.

vector

  • Si ∇ · V > 0 (si la divergencia es Positiva) eso significa que en el entorno minúsculo alrededor de ese punto nacen líneas de campo. En términos del agua de nuestra bañera, eso significa que del entorno del punto (del círculo) salen más líneas de las que entraron. Cuanto más grande sea el número positivo, más líneas «nacen», es decir, más intenso es el flujo de agua saliendo del círculo.

vector2.png

  • Si ∇ · V eso significa que en el entorno minúsculo alrededor de ese punto mueren líneas de campo. En términos del agua de nuestra bañera, esto significa que en el entorno del punto entran más líneas de las que salen. Una vez más, cuanto más pequeño sea el número negativo, más líneas «mueren», es decir, más intenso es el flujo entrante.

vector3

btn1 btn
btn

Gradiente ∇Φ: De Escalar a Vector

Oscar Rosas Deja un comentario

∇Φ

La gradiente es la primera operación diferencial vectorial que veremos (vaya que eso suena complejo, pero no te preocupes).

Pero vamos, ¿Qué significa sacar la gradiente? ¿A qué «cosa» puedo sacarle la gradiente?

Preguntas muy buenas Timmy, y también fáciles de responder:

  • ¿A qué «cosa» puedo sacarle la gradiente? A una función escalar. (Las de toda la vida pues).
  • ¿Qué significa sacar la gradiente? Es una operación en la que tu obtienes una función vectorial iniciando con una función escalar.
  • ¿Cómo? Así.

gradiente

Ok, ok, eso fue un cambio brusco, veamos si ahora que ya vieron la fórmula, la definición formal se ve más fácil de entender.

«El gradiente es una operación vectorial, que opera sobre una función escalar, para producir un vector cuya magnitud es la máxima razón de cambio de la función en el punto del gradiente y que apunta en la dirección de ese máximo.»

  • Observa que la gradiente de un campo escalar ∇Φ define un campo vectorial
  • De forma geométrica el gradiente es un vector que se encuentra normal (perpendicular) a la curva de nivel en el punto que se está estudiando.

Aquí un ejemplo:

Gradiente

Derivada Direccional

Una forma equivalente de definir el gradiente es como el único vector que, multiplicado por el vector unitario, da la derivada direccional del campo escalar:

derivada-direccional

Vector Normal a Superficie

Otro truco con la gradiente es que si tenemos una superficie como esta:

campo

Esto gradiente-icono es un vector perpendicular a la superficie , donde c es una constante.

Y eso, eso es todo amigos, ahora es hora de ver la siguiente operación vectorial, la divergencia.

btn1 btn
btn

Operador Nabla

Oscar Rosas Deja un comentario

Salve Dios Nabla

∇

Este símbolo triangular aparentemente básico se llama nabla.

Se trata de un operador matemático que puede tomar parte en diversas operaciones vectoriales. (Osea que los matemáticos usan este símbolo para representar muchas operaciones dependiendo del contexto, de la misma manera que tú y yo usamos la palabra banco).

banco2
banco

Nabla es un operador matemático muy versátil, que puede aplicarse a números normales y corrientes (como la temperatura en distintos puntos de una habitación) o a vectores (como nuestro famoso campo eléctrico), y es capaz de proporcionar información muy interesante sobre ellos.

En coordenadas cartesianas tridimensionales, nabla se puede escribir como:

nabla

Este operador vectorial posee propiedades análogas a las de los vectores comunes. Es útil para definir tres cantidades que aparecen en ciertas aplicaciones y que se conoce como gradiente, divergencia y rotacional.

Fin de la Lección.

Si, tenemos un problema, y es que tanto nabla como la gradiente, rotacional y la divergencia son temas muy rápidos y cortos, pero todos juntos serían estúpidamente largos, así que espero que el lector me perdone.

Así que empecemos con los temas:

Da click en el tema que quieras ver

btn1 btn
btn

Funciones y Derivación Vectoriales

Oscar Rosas Deja un comentario

Funciones

Siempre me ha gustado la idea de las funciones como cajas negras, usando esa idea una función vectorial no es más que una caja negra en la que tu metes uno o más números reales y obtienes del otro lado un vector.

funciones.jpg

¡Y ya!

Eso es todo….bueno, casi todo.

Bueno, otra forma de verlo es así:

funcion

¿Bonito, no? Pues sí, pero si quieres expresar tu función vectorial así tendrás que hacer un paso más, algo que será común hacer hasta el final. Parametrizar.

Parametrización y Funciones Paramétricas

Funciones Parámetricas: Son las funciones que describe como se mueve la partícula a lo largo de un eje del espacio y que dependen de un SOLO parámetro.

O un poco más aburrido:

» Este sistema de ecuaciones paramétricas permite representar una curva o superficie en el plano o en el espacio, mediante valores que recorren un intervalo de números reales, mediante una variable, llamada parámetro, considerando cada coordenada de un punto como una función dependiente del parámetro».

graph.png

Se debe destacar que para cada curva existen infinitas parametrizaciones posibles.

Así que..bueno, esto de parametrizar será un poco más difícil de lo que se veía.

Pero bueno, no importa, veamos que podemos avanzar mientras vamos viendo como parametrizar.

Derivación de Funciones Parametrizadas

Ahora, gracias a nuestro querido Schaum podemos empezar a Derivar

Primero usaremos a  A, B y C como funciones vectoriales diferenciables,  un parámetro u, y que Φ es una función escalar. Entonces se cumplen las leyes siguientes:

¡Y ya!

shaum

Formulas Basicas

Bueno, casí, porque ahora es momento de ver al Dios de esta materia.

El Bendito y todo poderoso Operador Nabla.

Da click aquí para descubrir y adorar al bendito Operador Nabla.

btn1 btn
btn

Producto Punto y Cruz

Oscar Rosas 3 comentarios
Anuncios

Ok, esto se esta poniendo interesante, ahora vayamos con un tema que muchas veces termina haciendo que odiemos la materia.

Empecemos por lo obvio, en Análisis Vectorial hay dos clases de productos, no como en las matemáticas de toda la vida ¿porque? ni yo lo se.

Lo que si se es diferenciarlos:

  • Producto Punto es cuando multiplicamos dos vectores y nuestro reultado es un escalar (un número, vamos).
  • Producto Cruz es cuando multiplicamos dos vectores y nuestro resultado así como en la suma es otro vector.

Así que empecemos con el más sencillo.

 

 

Producto Punto

El producto punto se llama así simplemente porque ponemos un punto para saber que estamos hablando de esa operación.

Bueno, ¿pero como la hacemos?

Muy buena pregunta, y es sencillo, sigan la formúla : )

punto

¿Y qué significa esto? ¿De dónde sale esto?

No tienes idea de cuanto, cuanto tiempo me tomo descubrir esto, y no se preocupen, que pronto les dire, pero antes veamos otra forma de hacerlo, como no, por componentes:

punto2.png

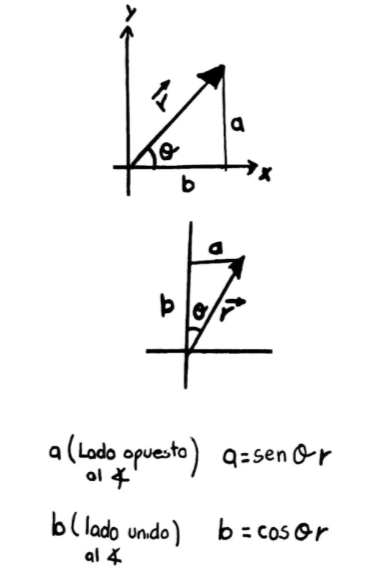
Es muy importante la parte de abajo, y les intentaré explicar que dicen mis dibujos, y es que basicamente cuando tu multiplicas las componentes puedes obtener dos resultados:

  • Si las compontentes que estas multiplicando son la misma (i • i , por  ejemplo) y entonces el resultado es un simple 1, no un vector ni nada, solo un 1.
  • Si no son las mismas, no le des mas vueltas, la respuesta es siempre 0.

Producto Punto y Cosas Perpendiculares

Este es un dato curioso (y muchas veces muy útil) es que si el producto punto te sale 0, es que ambos vectores son perpendiculares. SIEMPRE.

 

Producto Punto y Angulo

Se puede reordenar la fórmula del producto punto para poder facilitar encontrar el ángulo entre 2 vectores.

ángulo.jpg

 

¿De donde sale la fórmula del Producto Punto?

Ok, esto tal vez no se los vayan a preguntar en un exámen, pero siempre ayuda muchisímo saberlo, pues ya tienes un super interesante tema de conversación (… y luego me pregunto porque esto soltero XD).

Bueno, empecemos:

proyecccion.png

Proyección de A en B

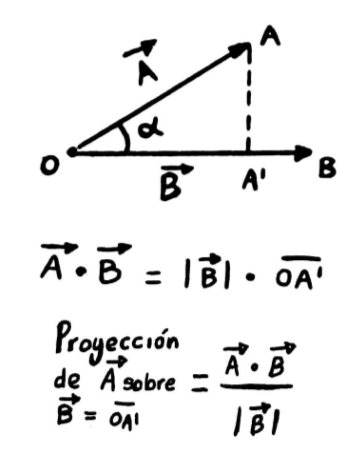
Este dibujo representa lo que nosotros vamos a llamar la proyección de un vector (en terminos mortales la «sombra» de un vector con respecto a otro» ).

Lo importante de este diagrama, es darte cuenta de donde sale el coseno, la proyección es simplemente A cos θ. ¡De ahí sale el coseno de a fórmula!

A continuación les dejo un montón de calculos matemáticos que no son necesarios que entiendan aún, pero quería ponerlos : )

proyeccion

Ahora sí, ya tenemos todo lo necesario para descubrir de donde salió la fórmula y es que vamos a verlo de forma gráfica (osea con más dibujitos ¡wiii!).

Forma Geométrica

«El producto de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él».

Esta es una definición más formal pero justo lo que necesitamos para entenderlo.

proy2

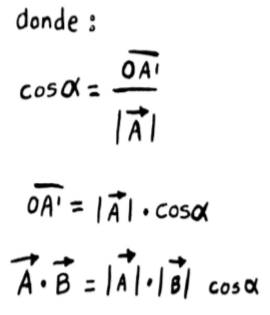
proy3.png

Y ¡bingo!

¿Qué demonios hiciste?

Seguí la definición, el producto punto es igual al módulo de uno de ellos por la proyección del otro sobre él, expandí un poco más que es la proyección usando los calculos de allá arriba y apareció el coseno juto como lo esperabamos, y llevamos a la formula que siempre hemos conocido.

¿Es necesario que entienda lo que acaba de pasar? Por supuesto que no, siempre es divertido, pero esta bien si no entendiste una pinola de lo que esta allá arriba.

Producto Cruz / Vector

«El producto vectorial de dos vectores es otro vector cuya dirección es perpendicular a los dos vectores».

No es una definición en sí pero nos sirve para empezar a trabajar.

¿Qué pasa si hacemos el producto cruz con puras componentes?

Fácil.

Esto.

cruz

Truco para el P. Cruz

Este es un pequeño diagrama que muestra que pasa cuando multiplicamos componentes con el producto cruz, así que vamos a explicar el diagrama:

  1. Pon tu dedo en el primer elemento a multiplicar
  • Si el segundo elemento es el que apunta la flecha entonces la respuesta es la componente a la que apunta la flecha que sale de tu segunda componente a multiplicar
  • Si el segundo elemento NO es el que apunta la flecha entonces la respuesta es el inverso de la componente que queda.

 

 

 

Tambien podemos entender el modulo o la magnitud del vector resultante como el área de la figura que forman los vectores.

cruz2.png

Sentido

Esto es mas dificil para mi del producto cruz…¡Saber a donde va, hacia arriba o hacia abajo!

No te preocupes, te daré una idea que espero que pueda ayudarte a entender esto mejor.

  1. Imaginate o dibuja ambos vectores en el plano.
  2. Si el camino de A a B es en el sentido de las manecillas del reloj entonces el vector resultante será hacia abajo.
  3. Si es en contra de las manecillas entonces será hacia arriba.
  4. ¡Listo!

¿No me crees? Pues por un lado entonces no se porque sigues haciendo leyendome, pero no importante, la ciencia no se basa en confianza pura y ciega, y eso es lo que me encanta, así que aquí esta la prueba.

Bueno, ¿pero como hacemos la operanción en sí?

Muy buena pregunta, y es sencillo, con eso del sentido fuera del camino, podemos volver a hacer unos esquemas con las fórmulas como las de arriba del producto punto, pero para el producto cruz.

cruzbien.png

O como no podría ser de otra manera, podemos sacarlo por componentes usando matrices (pronto tambien tendré una lección solo dedicada a esto).

Así que en resumen, pueden seguir la fórmula de aquí abajo, si les dan los vectores como componentes.

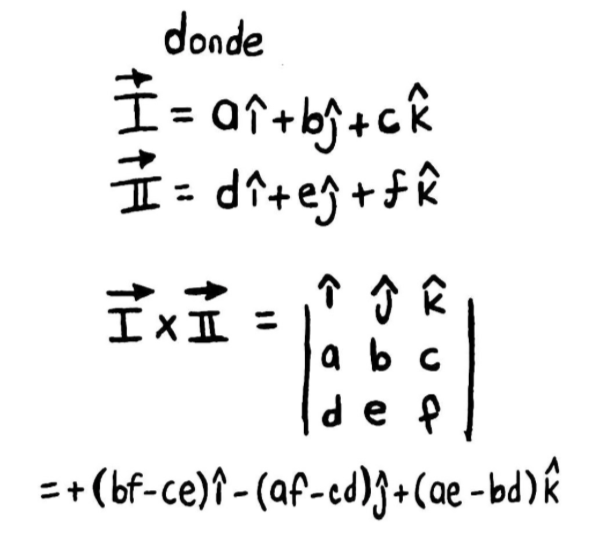
cruz5.png

Producto Cruz y Cosas Paralelas

Este es un dato curioso (y muchas veces muy útil) es que si el producto cruz te sale 0, es que ambos vectores son paralelos. SIEMPRE.

Producto Mixto

Esto no es mas que una clase algo rara de una combinación de ambos, pero si alguno lo necesita, aquí esta:

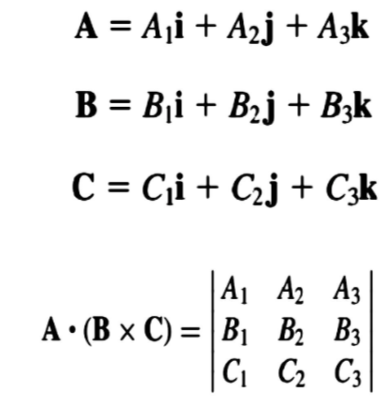
mixto.png

¡Listo! Ya podemos quitarnos las cosas básicas, es hora de empezar a ver como se deriva y se integran vectores…

¿O no?

Recuerdas como te dijeron en la prepa que el Cálculo era fundamentalmente el estudio (si a derivar e integrar le pueden decir estudio) de las funciones.

Pues bueno, para poder derivar e integrar,primero habrá que crear o descrubir (una duda clásica en mate) las FUNCIONES VECTORIALES. Así que vamos.

Da click para verlas y ver como diferenciarlas.

btn1 btn
btn
Anuncios

Álgebra Vectorial

Oscar Rosas Deja un comentario

Perfecto, si has llegado hasta aquí quiere decir que has llegado más lejos que el 90% de mis lectores, espero que el estilo de enseñanza (como te explico pues) te esté gustando.

Ahora que ya conoces a nuestro nuevo juguete, los vectores, veremos cómo podemos hacer álgebra con ellos.

PD: Si quieres ser Hardcore y ver de una vez el producto está aquí.

Sino, es hora de empezar.

 

 Igualdad Vectorial

  • Dos Vectores son iguales si tienen el mismo módulo, dirección y sentido.
  • Dos vectores son inversos si tienen la misma magnitud y dirección pero sentido opuesto.

inversos

 Suma Vectorial

suma

Ok, creo que eso fue estúpidamente fácil, así que espero que esto te resulte más interesante, la suma vectorial, primero te diré que llamaré S al vector resultante…pero ¿Cómo obtenerlo?

Por Método Gráfico (Del triángulo)

triangulo

Este es el método más sencillo de entender, y simplemente dice para obtener la suma debes seguir los siguientes pasos:

  1. Dibujar el primer vector como te de la gana
  2. Dibujar el segundo vector pero dibujando el origen del segundo vector en la flecha del primero. Y ya.
  3. Tu vector suma será entonces un vector que empiece en el origen de A, y termine donde esta la flecha de B.

Por Componentes

Como te estarás empezando a dar cuenta, mi método favorito es las componentes, ¿porqué? ya lo sabras cuando lleguemos a integrales *música drámatica*

Además es también igual de sencillo, simplemente suma las componentes de cada vector y listo :3

suma-en-3d

angulos

Magnitud

Y su magnitud se puede sacar de una manera muy parecida a como la habíamos visto antes, por cierto, esta fórmula se deriva del teorema de Pitágoras, espero algún día explicarles más sobre el tema.

magnitud

Ángulo Resultante

Este es el ángulo que tendrá nuestra resultante con respecto al eje X.

angulo

Para terminar la suma los dejos con algunas propiedades que siento que pueden resultarles útiles.

propiedades.png

 Resta Vectorial

Ok, ok esto les va a encantar, para hacer una resta simplemente sigan estos pasos:

  1. Saca el inverso del segundo vector
  2. Suma con el primero
  3. ¡Listo!

¿no me crees?

Mira :3

resta.png

Un escalar por un Vector

Esto ni siquiera la considero un producto vectorial porque es estúpidamente fácil hacerlo, solo sigan las ecuaciones de abajo.

algebra

¿Listo?

Esto se va a poner bueno, es hora de ver un clásico, producto cruz y producto punto.

Da click para la siguiente Lección: Producto Punto y Cruz

btn1 btn
btn

Vectores y sus Características

Oscar Rosas

vector

En este post veremos:

  • ¿Qué es un vector?
  • Dirección y Sentido
  • Magnitud
  • Vectores Unitarios
  • Componentes

 

Bienvenidos a la primera lección de Análisis / Cálculo Vectorial, vamos, empecemos:

» Un vector es una herramienta matemática que se representa por un módulo, una dirección y un sentido.» 

– Un libro muy importante y serio

tabla

También otra forma de entenderlo es pensar en un segmento (o pedazo) de recta, llamemosla PQ, donde P es el origen y Q el punto terminal.

Y si… eso es todo, explicar más a detalle esa definición es bastante complicado, es mucho más fácil aprender esto aplicando los conceptos, así que si, quédate con esa idea y veamos cómo cambian las matemáticas cuando cambiamos nuestros conocidos números de toda la vida (aquí les llamamos escalares) por nuestro nuevo juguete, los vectores.

Así que veamos las características más importantes de estos:

Dirección y Sentido

Esto es lo más difícil de este tema, (¡Recordar cual es cual!) así que en palabras sencillas para que lo recuerdes esto sería algo así:sentido

  • Dirección: Es la orientación que tiene el vector, es decir, sus ángulos con respecto a los ejes.
  • Sentido: Es hacia donde apunta el vector, es
    decir, por ejemplo, si apunta hacia el norte o al sur.

Magnitud / Norma / Módulo

El módulo de un vector es la longitud del segmento orientado que lo define… ósea, es el tamaño del vector.

modulo

Gracias a la formulita de arriba podemos deducir unas cuantas cosas importantes:

  • El módulo es un número siempre positivo.
  • Solo el vector nulo tiene módulo cero.

Vector Unitario

Ahora con todo esto entendido, podemos pasar al primer tema de verdad interesante, los vectores unitarios.

¿Pero qué demonios son? Muy fácil, primero, tenemos un vector normal A, entonces el vector unitario de A es un vector igualito a A, pero cuyo tamaño es sólo de uno.

vectores-unitarios

¿Y matemáticamente como lo calculamos?

Muy fácil, podemos encontrar nuestro vector unitario u simplemente dividiendo a A entre su magnitud.

unitarios

Ejemplo:

ejemplo

Vectores Unitarios a los Ejes

Ok, lo admito, no se donde poner este tema, si lo se, se que debería ir antes, pero espero que el lector me perdone.

En resumen, les contaré algo, podemos hablar de vectores en dos sentidos.

  • Dando su magnitud y un ángulo (Del estilo, un vector de 13N a 12 grados NE)
  • Dando sus componentes (Del estilo 3i + 5j +3k)

¿Quieren escuchar un secreto? Todos los matemáticos odiamos la primera, de verdad que la odiamos con toda nuestra alma -.- , así que te mostraré la segunda :3

ejes

Aquí está nuestro querido plano cartesiano, con sus 3 dimensiones X,Y,Z ; ahora a cada una de ellas le vamos adjuntar (o asociar) un vector unitario muy especial: i,j,k.

¿Por qué estas letras? La verdad ni yo lo sé, pero ya es una convención (ósea algo que usa mucha gente) en la materia, así que la usaremos para que puedan entender un libro sobre este tema sin demasiados problemas.

Ahora con esta nueva información podemos describir a un vector no por su magnitud y su sentido, sino como la suma o componentes en cada sentido….

¿no entendiste la última línea? No te preocupes, solo sigue leyendo, es normal.

unitarios

Componentes de Vectores

¿Y cómo demonios averiguo que númeritos poner en i,j,k si solo me dan su magnitud y un ángulo?

Esa es una excelente pregunta Timmy (si, te llamaré Timmy, te guste o no) para contestarla vamos a usar algo llamado componentes.

Las componentes de un vector son simplemente vectores que van sobre los ejes, tales que si sumo todos los componentes de un vector, obtengo el vector….Si, es mucho más fácil verlo que explicarlo:

Componentes en 2D

angulos

Componentes en 2D

Estas son las más sencillas, tendremos nuestro vector r (simplemente porque me canse de la A) y un ángulo con respecto al Eje X.

Nota: Al igual que por muchas cosas, por convención siempre medimos el ángulo de una vector con respecto al eje x, no me preguntes porque -.-

Entonces, para sacar cada componente, solo sigue la fórmula de abajo, estas se deducen de trigonometría (próximo curso de eso seguro).

Componentes en 3D

ejes-y-angulos

Componentes en 3D

Son basicamente las mismas que en 2D, solo que con un paso extra, primero, sacas un ángulo con respecto a Z, y respecto a este sacas una proyección.

Y trabajas esa proyección como si fuera un vector en el plano XY.

… O simplemente puedes seguir las fórmulas  ; )

¡Es mucho más fácil!

¡Perfecto!

meme

Has logrado llegar al final de la primera lección, las cosas ahora se pondrán mas interesantes, ya sabes que un vector y sus características, ahora veamos la siguiente pregunta:

¿Qué pasa si quiero sumar un vector?

Da click para la siguiente Lección: Álgebra Vectorial

btn1 btn
btn