Primera Parte
Segunda Parte
Ahora la Gran Confiable
Resulta que integrar no es tan fácil como parece, pero hay algunas técnicas que pueden ayudarte
Se trata de reescribir toda la integral en términos de una nueva variable, generalmente una letra que nadie usaría de forma normal : U, es decir:
Recuerda:
No pongas límite (en caso de tenerlo) hasta terminar de Integral
¿De donde sale la fórmula? Esto es de verdad muy útil de saberlo, veamos:
Ahora viene la pregunta del millón:
La forma más sencilla es aprenderse esta tabla y tenerla a la mano por cualquier cosa:
Bienvenidos al tema más estúpidamente largo de esta materia, pero no te preocupes, todo estará bien.
El primer paso es ver como es ver si debemos dividir la expresión o no, para hacerlo, basta con ver el grado de los polinomios:
Para saber que hacer ve el grado
Para Factorizar Q(x) haremos esto:
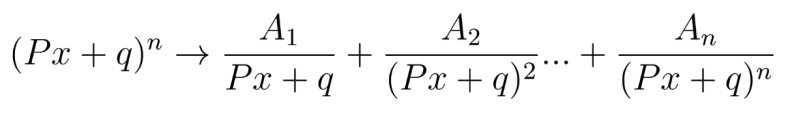
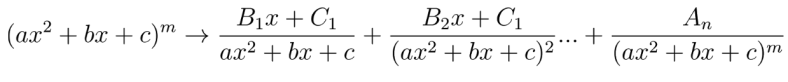
Recuerda que la derivada es un operador Lineal:
Da lo mismo sacar la integral de una suma de funciones que sumar la integral de ambas funciones.
Da lo mismo sacar la integral de una una función por una escalar que multiplicar la integral de esa función por el escalar.
Es decir visualmente como:
Visualmente
Las más básicas
Las Exponenciales
Las Trigonométricas
Las reciprocas
Las endemoniadamente útiles
Están será útiles … pero raras :
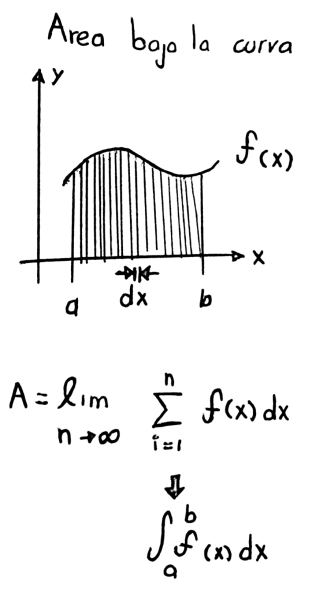
Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
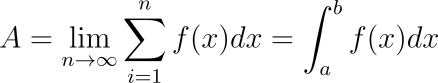
A continuación les muestro varios teoremas que quia encuentras muy útiles:
Recuerda que la derivada es un operador Lineal:
Da lo mismo sacar la integral de una suma de funciones que sumar la integral de ambas funciones.
Da lo mismo sacar la integral de una una función por una escalar que multiplicar la integral de esa función por el escalar.
Es decir visualmente como:
Visualmente
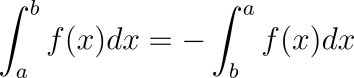
Imaginate la siguiente función.
Si alguien malvado te preguntará (alguien malvado…) ¿Dónde esta el punto máximo en esa función?
Tenemos varias opciones:
…O ser inteligente y usar el calculo para encontrar la respuesta:
*Tu función debería ser continua en el intervalo en el que estés pensando para que lo que vaya a decir tenga sentido…digo, sino no tiene sentido nada de lo que digo.*
Podemos definir entonces que los puntos críticos de nuestra función son cuando:
Gracias a lo que vimos podemos sacar la derivada y obtener muchas respuestas:
Como que de la última formula podemos saber que la función:
Así como la primera derivada nos muestra sobre como va la función, si crece o decrece, la segunda derivada, nos habla de como cambian esos aumentos y reducciones.
Esto se conoce en matemáticas como Concavidad.
Tipos de Concavidad (Palabrería)
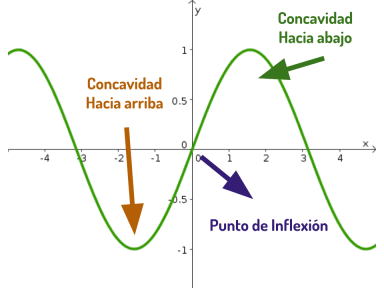
Puntos importantes en la Gráfica
Si una función f(x) tiene un máximo o mínimo cuando x = c, entonces x = c es también un punto crítico.
Así que si queremos encontrar los máximos o mínimos:
Puedes acceder al texto original, si le picas en PDF:
Texto de Referencia
Dado una función de f(x), tenemos dos diferenciales, y estos guardan una relación muy importante, recuerda que tenemos dos notaciones para la derivada:
Esto nos dice algo super genial: La derivada no es más que la razón entre dos diferenciales.
Así que gracias a esto podemos sacar la relación entre estas diferenciales, por ejemplo para la diferencial de y:
Veamos algunos ejemplos:
Ahora podemos ocupar los diferenciales para encontrar errores:
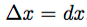
Si pensamos en ∆x como el cambio infinitesimal en x, podemos ver que el cambio en y se puede obtener de:
Si ∆x es pequeño entonces así lo será ∆y, solemos llamar a esto «errores».
Los «errores» miden cambios en y en x.
Esfera: Una esfera fue medida y su radio es de 21 u con un error posible máximo de 0.05 u. Calcula el posible error máximo.
Antes que nada (y para que no me coman antes de nada), las demostraciones de todo lo que estoy diciendo están abajo, pero ahora empecemos por lo bueno, las formulas:
Ahora y antes de seguir, tienes que saber que hay muchas, muchas maneras de escribir esta operación… muchas:
Antes que nada supón esto …
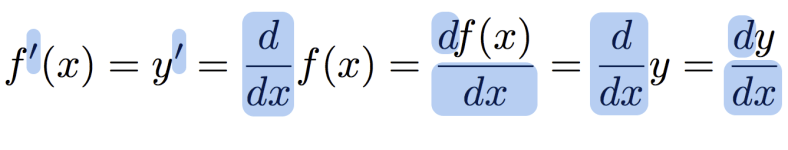
Las mil y un derivadas (Formas del Operador Derivada)
Recuerda que la derivada es un operador Lineal:
Da lo mismo sacar la derivada de una suma de funciones que sumar la derivada de ambas funciones.
Da lo mismo sacar la derivada de una una función por una escalar que multiplicar la derivada de esa función por el escalar.
Es decir visualmente como:
Esto siempre se conserva
Las de memoria
Las clásicas
Una interesante pero no conocida
Recuerda esta «simplificación» para que sea mas sencillo:
Simplificaciones
Suma (O Resta) de Funciones
Producto de Funciones
División de Funciones
Repite después de mi: «La derivada de la composición de dos funciones es igual a: La derivada de la primera función evaluada en la segunda multiplicada por la derivada de la segunda«.
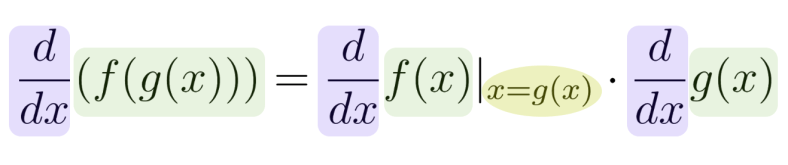
Esta Formula es como tu Biblia
Aquí hay un par de cosas que me gustaría contarles:
Se puede derivar una función más compleja si se usa una variable intermedia y luego se multiplica por la derivada de dicha variable.
Potencias de Funciones
Raíces de Funciones
Raíces
Exponenciales
Logaritmos
Básicas
Las reciprocas
Las inversas 😀
Las inversas de las reciprocas (que complejo suena eso D:)
Compilando Conocimiento 