Cambio de una Función: Derivada
Imaginate la siguiente función.

Si alguien malvado te preguntará (alguien malvado…) ¿Dónde esta el punto máximo en esa función?
Tenemos varias opciones:
- Podemos tabular algunos valores hasta encontrar uno que creamos que sea el máximo (o mínimo).
- Podemos graficar y empezar a tantear por donde esta el máximo.
- Llorar, llorar siempre es una opción.
…O ser inteligente y usar el calculo para encontrar la respuesta:
*Tu función debería ser continua en el intervalo en el que estés pensando para que lo que vaya a decir tenga sentido…digo, sino no tiene sentido nada de lo que digo.*
Función Creciente y Decreciente

- Si la derivada en x es mayor a cero entonces quiere decir que la función esta creciendo en x.
- Si la derivada en x es menor a cero entonces quiere decir que la función esta decreciendo en x.
Puntos Críticos
Podemos definir entonces que los puntos críticos de nuestra función son cuando:
- Nuestra primera derivada es cero (es decir, no crece ni decrece).
- Nuestra primera esta indeterminada.
Gracias a lo que vimos podemos sacar la derivada y obtener muchas respuestas:


Como que de la última formula podemos saber que la función:
- Siempre va a crecer desde -1 a 0 y desde el 2 al infinito.
- Siempre va a decrecer desde el menos infinito hasta el -1 y también desde 0 hasta 2.
Concavidad: Segunda Derivada
Así como la primera derivada nos muestra sobre como va la función, si crece o decrece, la segunda derivada, nos habla de como cambian esos aumentos y reducciones.
Esto se conoce en matemáticas como Concavidad.

Tipos de Concavidad (Palabrería)
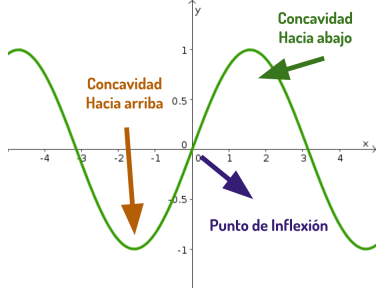
Puntos importantes en la Gráfica
Concavidad Hacia Arriba / Abajo

- Si la segunda derivada en x es mayor a cero entonces quiere decir que la función tiene una concavidad hacia arriba.
- Si la segunda derivada en x es menor a cero entonces quiere decir que la función tiene una concavidad hacia abajo.
- Punto de Inflexión: Podemos decir entonces que un punto de inflexión es cuando la concavidad de la función cambia.
Teorema de Fermat (quien sabe cual sea)
Si una función f(x) tiene un máximo o mínimo cuando x = c, entonces x = c es también un punto crítico.
Máximos y Mínimos (Receta de Cocina):
Así que si queremos encontrar los máximos o mínimos:
- Calcular los puntos críticos, es decir derivar f(x)
- f’(x) =0 , es decir Igualar a 0 la 1° Derivada
- Resolver la ecuación (que salir del paso 2) y obtener las raíces
- Calcular la segunda derivada
- Sustituir las raíces en la 2° derivada y comparar resultados
- Si Resultado < 0 Máximo
- Si Resultado > 0 Mínimo
