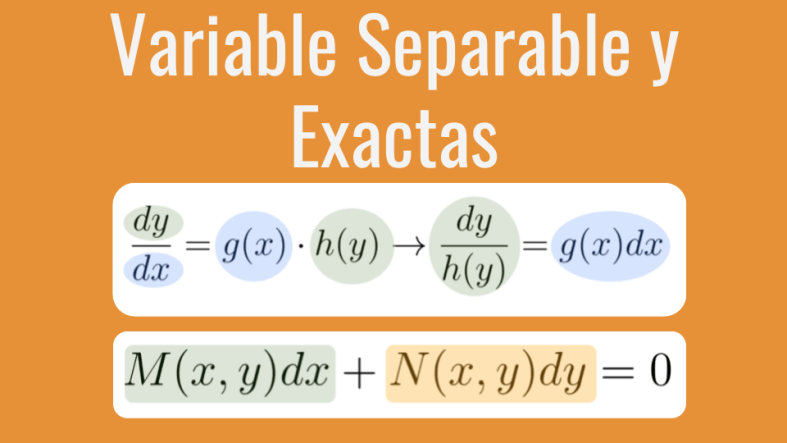Autor Oscar Rosas
Ecuaciones usando series
Transformada de Laplace 4
Transformada de Laplace 3
Transformada de Laplace 2
Transformada de Laplace
Metodo del Eliminador
Este método es super, super genial para verlas, lo que tenemos que hacer es primer ver que tu ecuación esta escrita de esta forma:
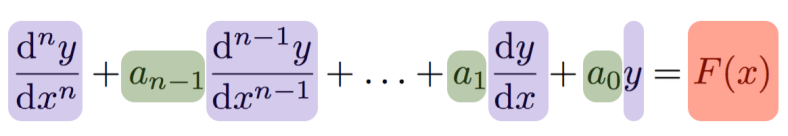
Esta ecuación es aplicable al metodo del Aniquilador
Podemos aplicar el Aniquilador si podemos eliminar (o aniquilar F(x))

Conozcan al Aniquilador
Como la forma de lograr esto es muy «vaga» solo puedo dar pasos generales:
- Elimina la parte derecha de la ecuación
- Resuelve como siempre la parte homogénea
- Compara con la parte homogénea que encontraría de manera «normal» para ubicar a la Parte Particular
- Iguala tanto la parte derecha original como la parte que encontraste que era Particular
- Encuentra el Valor de las Constantes
Aniquiladores


Veamos porque sirven:
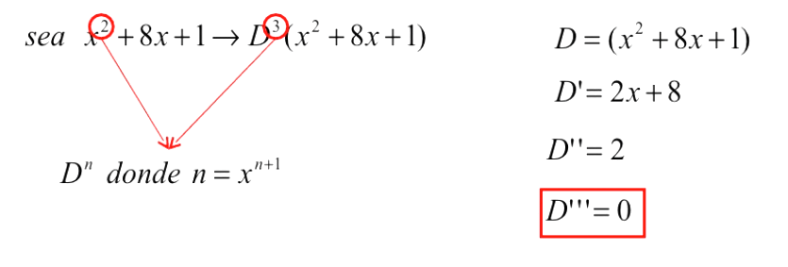
Anulador
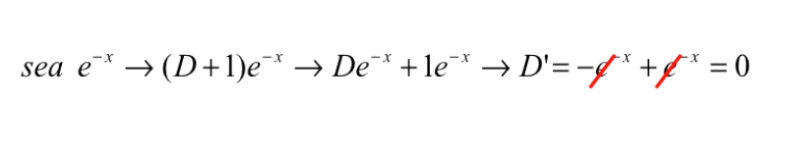
Anulador
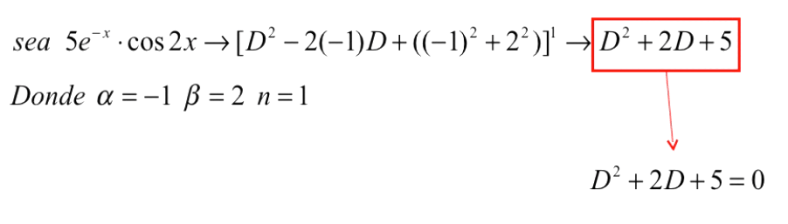
Anulador
Ejemplo:

Anulador

Polinomio Característico
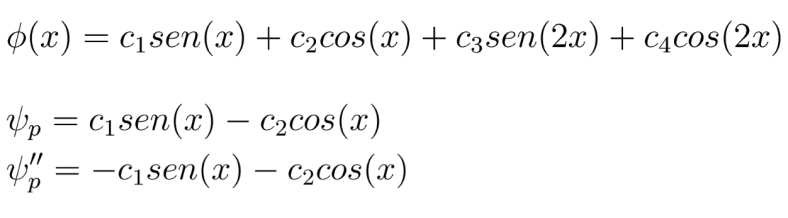
Encontrar la Parte Particular

Final Respuesta
Ecuaciones de Orden Superior Variación de Parámetros
Estas ecuaciones son ecuaciones diferenciales que no son de primer orden, es decir en las que tenemos involucradas segundas, terceras, etc.. derivadas.
Estas se complican más pero curiosamente son más mecánicas (y por lo tanto para mucha gente más sencillas).
A continuación se presentan varias formas de solucionarlas:
Homogéneas
(Órden 2)
Recordemos, que a una ecuación la llamemos Homogénea cuando esta igualada a cero.
Nota: Para empezar a explicar estas ideas usaré de base que estamos trabajando una ecuación de grado dos, al final del articulo contaré como subir a ordenes superiores.
Estas son las más sencillas de todas, incluso mucho más que varias de primer orden incluso. Veamos, una ecuación diferencial lineal de orden 2 homogénea la podemos escribir así:
PASO 1: La Ecuación Original

Ecuación Original: Así recibimos el problema
PASO 2: Encontremos las soluciones del Polinomio Característico
A cada ecuación tenemos un «polinomio característico» que podemos escribir así:

Este es el polinomio que tenemos que igualar a cero para encontrar raíces
Esto nos da mucha información, la parte interesante de todo esto es encontrar sus raíces, así que antes de seguir, veamos varias técnicas que quizá te ayuden a encontrar las soluciones a dicho polinomio.
Recuerda: Encontrar las raíces de un polinomio no es mas que igualo a cero y encontrar todos los valores de r que cumplen dicha igualdad.
Quizá Ayude: Raíces Cuadradas de Complejos
Supongamos que llegamos a un punto en el que tenemos que encontrar la raíz cuadrada de un número complejo…

Podemos hacer un poco de Álgebra y ver que para encontrar estos valores, solo tenemos que hacer un sistema de ecuaciones:

Pero lo más fácil siempre es la formula directa, aquí la tienes:

Fórmula Super Pro
PASO 3: Armar las Phi’s
La respuesta de nuestra ecuación tendrá muchas partes, cada una de ellas las denotamos con la letra phi , cada phi esta relacionada a una raíz, por eso era necesario sacarlas, ahora, sin mas veamos como quedan las phi:

Formulazo (Supon r son las raíces del polinomio)
PASO 4 – FINAL: Armar la Solución «Homogénea»
La solución homogénea es bastante sencilla de encontrar con TODO LO QUE YA SABEMOS , ya que todas las soluciones tienen esta forma:

Esta es la solución a nuestro problema : `)
Ejemplo:
Veamos un ejemplo:

Generalización de Homogéneas
Incluso podemos encontrar una solución mas general en la que para una ecuación de n grado, encontramos su polinomio asociado, y sacamos las raíces.
Supongamos que tenemos una raíz de multiplicidad m (osea que se esta raíz se repite m veces), entonces para esa pura raíz tendríamos m phi’s asociadas a ella, cada una de la forma:

Donde k varía de 0 a m-1, y r es la raíz repetida.
Homogéneas: Caso Especial – Raíces Complejas
En estos casos podemos hacer más cosas, así que veamos que pasa en este caso especial: Vamos a simplificar esto aún más, imaginate que tenemos la siguiente expresión:
PASO 1: La Ecuación Original

Donde las a’s son dos números reales cualquiera
PASO 2: Raíces
Ahora supongamos que las raíces del polinomio característico:

Veamos como encontrar esas misteriosas alfa y beta:
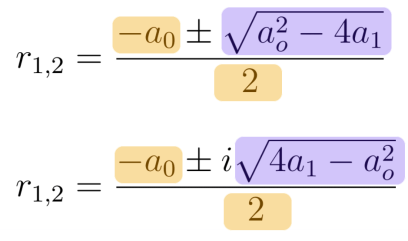
Y ya solo de formulazo tenemos que:

PASO 3 – 4: Armar las Phi’s
Nota: Euler
Para entender estohay que saber antes las que consideramos las identidades de Euler:

Euler Rocks papu!
Usando lo que ya sabemos si que podemos llegar a saber de donde salió la Formula Re Util:
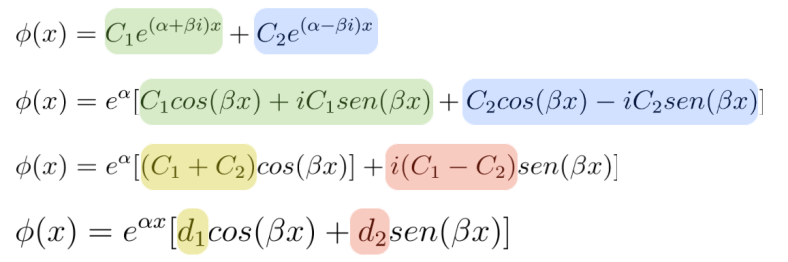
No olvides que d2 es imaginario : )
PASO 4: La Solución
Ahora podemos saber que ver que cualquier solución de escribe de la siguiente fórmula:

Formula Re útil
Variación de Parámetros: Constantes
(Órden 2)
Nota: Dependencia Lineal
Antes que ver los pasos tenemos que saber algunas cosas:
Dos funciones definidas en un invervalo, son linealmente dependientes en I, si existen dos constantes (diferentes de cero) tal que:
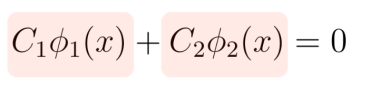
Y esto se cumple para todas las x dentro de ese intervalo.
Nota: Independencia Lineal
Dos funciones definidas en un intervalo, son linealmente dependientes en I, si las únicas dos constantes que cumplen para todas las x dentro del intervalo que:
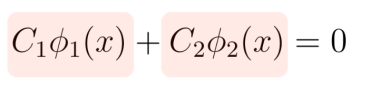
Son (redoble de tambores) que ambas constantes son cero.
Notas: Wronskiano
Dos soluciones de phi1 y phi2 de L(y)=0 son linealmente independientes en Intervalo si y solo si lo siguiente es distinto de cero:

Por ejemplo si suponemos que las raíces son diferentes podemos hacer este formulazo:
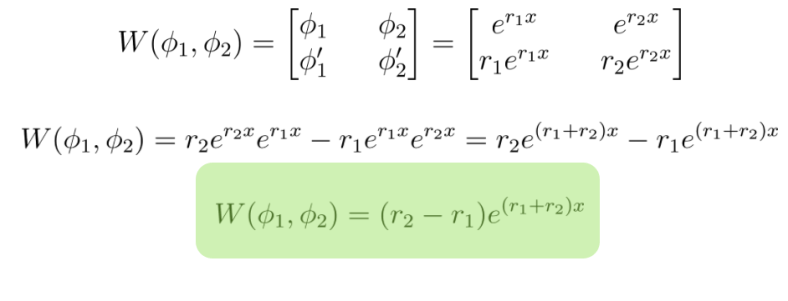
Formulazo para cuando las raíces son diferentes : ‘ )
Para todas las x en el intervalo existe algo llamado Wronskiano de phi1 y phi2.
Si phi1 y phi2 son solucion de L(y) = 0 sobre algun intervalo, contiene un punto Xo, entonces:

Ejemplo de sacar un Wronskiano:
Veamos si estas dos funciones son dependientes:

Como ves, son independientes.
PASO 1: La Ecuación Original
Considera la seguinte ecuación que se parece mucho a lo que acabamos de hacer:

Ecuación Original
PASO 1.1: Entender como irá la Solución
Podemos re bautizar a lo que habidos hecho con las ecuaciones homogéneas, para que veas que la solución a LA ECUACIÓN QUE ACABO DE PONER bien esta fórmula:

O visto de otra manera queremos esto:

Otra forma de ver la solución
PASO 2.0: Encuentra la Parte Homogénea
Y recuerda la solución de la parte homogénea ya sabemos como sacarla

Esta es la parte homogénea
Así que ahora iguala tu ecuación original a cero y ve a encontrar tu solución como si fuera una ecuación homogénea de las de arriba, orale!
PASO 2.0.1: ENTENDER la Parte NO Homogénea
Ahora lo que queremos es encontrar una solución tal que:

Solución que cumpla con esto
Ahora solo queda expandir un poco lo que acabamos de decir:

Derivadas

Evaluando la función
Bueno, de la expresión terriblemente larga de arriba podemos deducir que:

Finalmente podemos saber ya que:

De forma diferencial
PASO 2.1: Encontrar las U’s
Y esas u’s salen de:

Formulazo
PASO 2.2: Armar la Parte Particular de la Solución
Esta parte tendrá la siguiente forma:

PASO 3: Armar la Solución Final
Recuerda, ya solo tiene que escribir tu solución, ya tienes ambas partes :

O visto de otra manera queremos esto:

Otra forma de ver la solución
Notas: Ejemplo de este Tipo
Resolvamos la ecuación diferencial  :
:
- Primero hallemos la solución asociada a la ecuación homogénea
 . Su polinomio característico es
. Su polinomio característico es  , cuyas raíces son
, cuyas raíces son  y
y  . Como
. Como 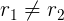 , la solución homogénea es:
, la solución homogénea es:
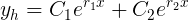
- Ahora vamos a hallar la solución particular. Sea
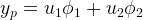 , donde
, donde 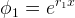 y
y  son las soluciones que hallamos anteriormente. Calculemos el Wronskiano:
son las soluciones que hallamos anteriormente. Calculemos el Wronskiano:

- Vemos que
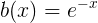 , por lo tanto, usando el formulazo llegamos a:
, por lo tanto, usando el formulazo llegamos a:
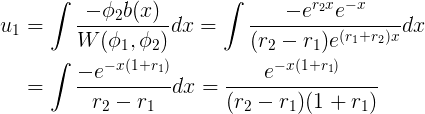
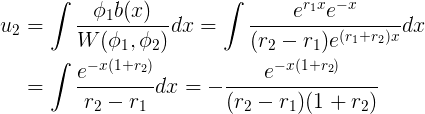
- Así, la solución particular queda como:

- Sustituímos los valores de las raíces y llegamos a:

- Para que se vea más bonita nuestra solución homogénea, podemos aplicar los resultados de la sección anterior:
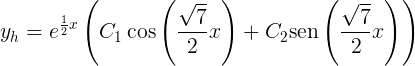
- Ahora sí, armamos nuestra solución general:

Lineales, Bernoulli y Ricatti
Ecuaciones Diferenciales Lineales
Son las que siguen este patrón:

PRIMER PASO: FACTOR INTEGRANTE
Hay que multiplicar toda la ecuación por una factor especial (factor integrante), este se calcula así:

Este es el Factor Integrante
¿Y de donde sale esta fórmulita?
Esta fórmula para encontrar el factor integrante se puede obtener de suponer que existe un factor integrante, y que si lo multiplicamos en la ecuación original tendríamos que:
![]()
Ademas podremos ver que esta expresión es valida:

Comparando ambas ecuaciones tenemos que:
Por lo tanto:

SEGUNDO PASO: ENTENDER EL DESPEJE
Multiplicar toda la ecuación por este término, y ve que el termino de la izquierda se puede SIEMPRE simplificar como derivación de un producto.
Podemos automatizar el siguiente proceso llegando a esta formula maestra:

Encontrando el gran formulazo
TERCER PASO: APLICAR EL FORMULAZO
Así, en resumen si tienes una ecuación diferencial lineal la solución siempre será:

MEGA FORMULAZO SI NO OLVIDAS EN +C
- PD: Nunca olvides el +C, ¡NUNCA OLVIDES EL +C!
- PD2: Nunca olvides esto:

Ejemplo:

Paso 1:
![]()
Paso 2 y 3:

Ecuaciones Lineales Homogéneas
Podemos hacer una excepción cuando Q(x) = 0, en este caso podemos reducir todo el proceso y encontrar que la solución simplemente es:

Ecuación de Bernoulli
Una ecuación diferencial de la forma:

Bernoulli papa
Es mejor conocida como la ecuación de Bernoulli.
Vemos que cuando n=0 ó n=1 se reduce a una ecuación lineal que ya hemos estudiado antes. (Así que no nos interesaría). Pero sino es ninguno de estos dos casos, entonces se puede hacer esto:
¿Cómo resolverla?
PASO 1: ELIMINAR POTENCIAS
Vamos dividir ambos lados entre y^n y hacemos una sustitución u= y^(1-n):

PASO 2 : SUSTITUCIÓN PAPU
Ahora aplicamos la siguiente sustitución y sustituimos en la original:


Paso 3: SOLUCIONAMOS COMO LINEAL
Esta última ecuación se convierte en lineal en la función u(y) si multiplicamos ambos lados por (1-n):

Buscando una forma más fácil de Solucionarlas
PASO 1: FACTOR INTEGRANTE
Vemos que el factor integrante es:
PASO 2: ENTENDER EL DESPEJE FORMULAZO
Por lo tanto, la solución viene dada por:

PASO 3: APLICAR FORMULAZO
Finalmente, deshacemos el cambio y llegamos a una formula super genial:

La maestra
Ejemplo:
Veamos la ecuación:

Encontremos el factor integrante:

Apliquemos formulazo:

Ecuación de Ricatti

Cuando tienes una ecuación como esta resulta que es imposible resolvería con lo que sabemos hasta ahora, así que tendremos que pensar de otra manera:
Para resolver una de estas NECESITAMOS una solución particular, ya que sin eso, es imposible hacer nada.
Pensemos en y1 como una de las soluciones.
PASO 1: PROBAR LA SOLUCIÓN
Prueba que y1 sea una solución.
PASO 2: DA EL CAMBIO PARA QUE SEA LINEAL

PASO 3: SOLUCIONA COMO LINEAL Y REGRESA A «y» AL FINAL

Ejemplo:

Hagamos esta Ecuación Lineal

Las soluciones salen de Ecu. Lineales
Variables Separadas y Exactas
Primero empecemos con algo que nos vendría muy útil aplicarlo siempre que podamos, las:
Ecuaciones de Variable Separada
Resulta que hay muchas maneras de escribir estas ecuaciones, podemos ir de una forma a otra con algo de álgebra, pero para que las conozcan les pondré sus formas mas conocidas:
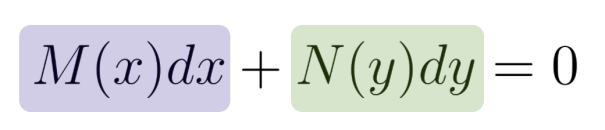
Veamos como resolverlas:
PASO 0: ORDENA TU ECUACIÓN
El paso más largo de resolver esta ecuación es curiosamente colocar tu ecuación de la manera en la que esta arriba:
FORMA 1:

FORMA 2:

PASO 1: INTEGRA CON RESPECTO A CADA DIFERENCIAL
Ya que la has llevado a la forma necesaria, basta con hacer esto:

Ejemplo:
Dada la siguiente ecuación, despejamos e integramos como dijimos arriba:

Y ya al final solo ponemos a nuestra respuesta bonita :3

De Ecuaciones Homogéneas a Separables
Si una ecuación tiene esta propiedad entonces cumple con esta característica tan rara:
Si tu evaluar esa función con «x» y «y» multiplicada por una constante t eres capaz de reescribir tu función para factorial esa t (elevada a alguna potencia) entonces decimos que tu ecuación es homogénea.

Y decimos ese es de grado algo, osea, que si ese algo es cero, es de homogénea de grado cero, si es dos es homogénea de grado dos y así.
Una ecuación diferencial de primer grado se dice que es homogénea si es que cumple con que ambas funciones M(x,y) y N(x,y) sea homogéneas y del MISMO grado.

¿Y porqué me debería interesar un comino eso?
Porque podemos hacer CUALQUIERA de los siguientes cambios de variable y podemos reducir esta ecuación a una de variables separadas.

Ejemplo:


Reducción Separación de Variables
Si tenemos una ecuación del estilo

SIEMPRE se puede reducir a una de variables separadas cuando este cambio.

Y que se existe una función f(u), luego sacas su diferencial df(u) e igualas a dy/dx. Finalmente ya solo resuelves por variables separadas.
Ejemplo:



Ecuación Diferenciales Exactas
Son las que podemos denotar de la manera:

Para estar seguro que sean ecuaciones exactas, tenemos que hacer un paso más y es que:
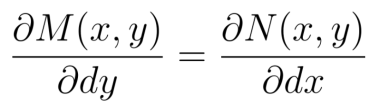
Forma de comprobar
Si esto es cierto entonces podemos hablar entonces que tanto M(x,y) como N(x,y) son derivadas parciales de una función más básica, una f(x,y):

Esta es la verdadera identidad de nuestras funciones
Así que nuestro objetivo es ahora encontrarla:

Forma de solucionarlas
Ejemplo:
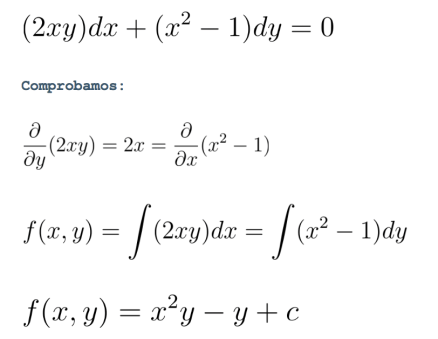
Para comprobarlas basta con sacar la diferencial de esta función, recuerdas como es que era para una función normal:

Diferencial Normal
Entonces para nuestra función sería algo así:

De aquí sacamos nuestra ecuación original
Forzar una Ecuación Exacta
Pero… y si quisiera que la ecuación que tengo fuera exacta, pero no lo es ¿Puedo «forzar» a que lo sea?

- Mu es la salvación
Pues si y no.
Para empezar, hay que encontrar si a nuestra ecuación la podemos forzar a ser, hay que encontrar el… Factor Integrante.
Para encontrarlo hay dos opciones, que sea por x o por y, así que veamos ambos casos:
Caso de X – Factor de X
Si el Factor es una función de X se tiene que cumplir que la siguiente operaciones nos arroje una función que solo depende de X.

Y entonces nuestro factor se puede calcular de manera muy fácil como:

Caso de Y – Factor de Y
Si el Factor es una función de Y se tiene que cumplir que la siguiente operaciones nos arroje una función que solo depende de Y.

Y entonces nuestro factor se puede calcular de manera muy fácil como:

Ahora vamos a hacer nuestra Ecuación Exacta
Y ahora, ya solo hay que multiplicar tu ecuación por ese factor y ahora tu nueva ecuación (SI TIENES TIEMPO COMPRUEBALA) es seguro que es exacta. 100% real, no fake.
Con esta nueva ecuación diferencial que ya es exacta, solo basta con usar el mismo método que el normal.
Veamos un ejemplo MUY resumido: