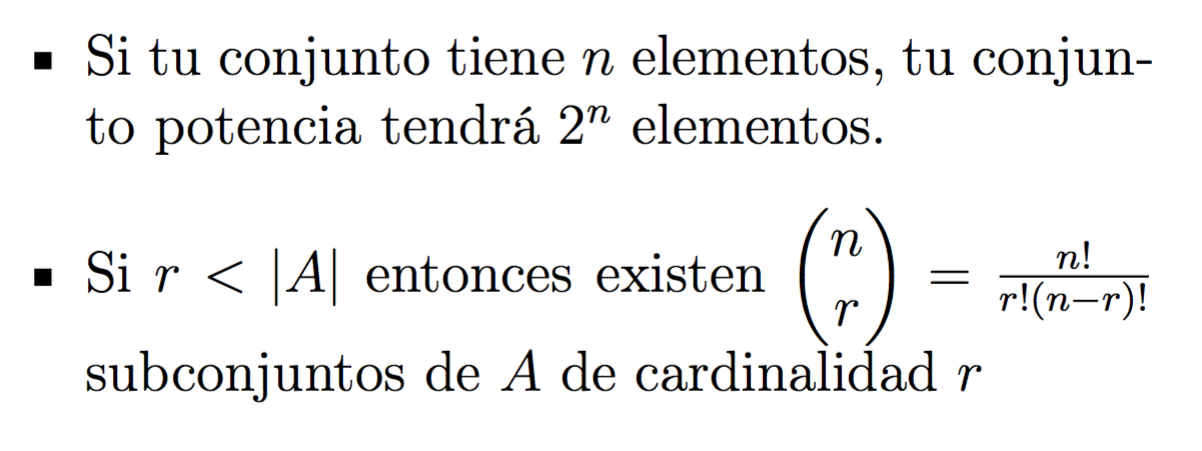
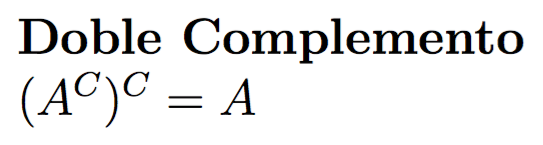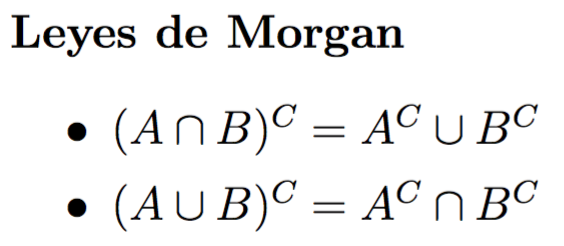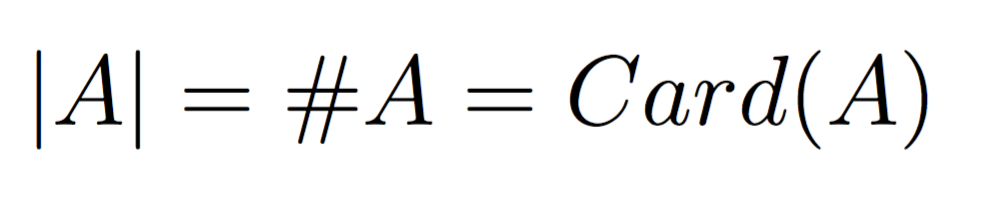Inducción Matemática

1 enero, 201711 octubre, 2020Oscar Rosas Deja un comentario

Anuncios

Principio de Inducción Matemática

La inducción para los matemáticos

La inducción matemática es un método de demostración que se utiliza cuando se trata de establecer la veracidad de una lista infinita de proposiciones.

El método es bastante natural para usarse en una variedad de situaciones en la ciencia de la computación.

Es decir, esta es (por favor no me maten matemáticos) su truco mejora guardado para demostrar proposiciones, esta es la oca de los huevos de oro.

También podemos ver a la inducción como una herramienta muy poderosa, una espada a máximo nivel, un arma en diamante en COD, tu y yo sabemos que el arma es poderosa, ahora te enseñare a usarla.

¿Cómo usamos la inducción?

Bueno, incluso podemos convertirlo en un «algoritmo», pero antes te comentaré que como todas las armas en los juegos no pueden estar tan OP (poderosas pues), así que te diré la debilidad de esta arma: SOLO FUNCIONA PARA LOS NÚMEROS NATURALES.

Una proposición $p(n)$ es verdadera para todos los valores de la variable $n$ si se cumplen las siguientes condiciones:

Paso 1 (Caso base): La proposición $p(n)$ es verdadera para $n = Natural$ .
Paso 2 (Hipótesis de Inducción): Se supone que $p(k)$ es verdadera , donde $k$ es un número natural cualquiera.
Paso 3 (Tesis de Inducción): Se demuestra que $p(k+1)$ es verdadera, es decir, $p(k) \implies p(k+1)$ .

Así se demuestra que la proposición $p(n)$ , para todo $n \in \mathbb{N}$ .

¿…Cómo?

Los 3 pasos de la inducción también se pueden escribir como:

Caso Base: Toma tu proposición, y encuentra un caso base, es decir el natural más pequeño que cumple la proposición.

Nota: Muchas, muchísimas veces es ese número es uno (ósea siempre se cumple), pero no siempre, así que no te confíes, encuentra ese caso base.

Supone que se cumple para k: Este es el paso más simple, lo único que tienes que hacer es creer (tratar como un axioma, como tu quieras verlo) que se cumple para el caso k.

Demuestra k+1: No todo en la vida podría ser tan fácil, este paso el el 95% de la dificultad del problema, usando lo del paso anterior tienes que demostrar que si se cumple para k A FUERZAS se cumple para K+1.

Si lograste llegar hasta aquí puedes decir con toda confianza que: DICHA PROPOSICIÓN ES VERDADERA (para todos los naturales : p) DESDE EL CASO BASE HASTA EL INFINITO.

¿Porqué funciona?

Podemos relacionar este poderoso principio con la analogía de las piezas de dominó: supongamos que tenemos una infinidad de piezas acomodadas, una detrás de la otra.

Ahora, si tiramos la primera, empujará a la segunda ocasionando que también caiga, esta a su vez empujará a la tercera y así sucesivamente, por lo que todas las piezas caerán.

El tirar la primer pieza es demostrar el caso base, y el demostrar si una pieza cae la siguiente también va a caer, es demostrar que $p(k) \implies p(k+1)$ .

Ejemplo #1

Problema. Demuestre que la suma de los primeros $n$ números naturales es $\dfrac{n(n+1)}{2}$ .

Solución. Vemos que la proposición que tenemos que demostrar es $\displaystyle \sum_{i=1}^{n} i = \dfrac{n(n+1)}{2}$ . Realizemos los tres pasos para demostrarla mediante inducción:

Paso 1: Para $n=1$ tenemos que $\displaystyle \sum_{i=1}^{1} i=1$ , y por otro lado $\dfrac{1(1+1)}{2}=1$ , por lo tanto la proposición es cierta para $n=1$ .
Paso 2: Supongamos que la proposición es verdadera para cualquier $k \in \mathbb{N}$ , es decir, supongamos que $\displaystyle \sum_{i=1}^{k} i = \dfrac{k(k+1)}{2}$ .
Paso 3: Probemos que la proposición es cierta para $k+1$ , es decir, probemos que $\displaystyle \sum_{i=1}^{k+1} i = \dfrac{(k+1)((k+1)+1)}{2}=\dfrac{(k+1)(k+2)}{2}$ . Al separar el último término de la suma tenemos que:

$\displaystyle \sum_{i=1}^{k+1} i=\sum_{i=1}^{k} i+(k+1)$

Pero por la hipótesis de inducción tenemos ahora:

$\displaystyle \sum_{i=1}^{k+1} i = \dfrac{k(k+1)}{2}+(k+1)$

Lo que resta es simple álgebra para llegar a la expresión deseada, factorizando y reacomodando tenemos que:

$\displaystyle \sum_{i=1}^{k+1} i = (k+1)\left(\dfrac{k}{2}+1\right)=\dfrac{(k+1)(k+2)}{2}$

Finalmente, por el principio de inducción matemática, se cumple que $\displaystyle \sum_{i=1}^{n} i = \dfrac{n(n+1)}{2}$ , para toda $n \in \mathbb{N}$ . $\quad \square$

Problema para el lector

Demuestre que la suma de los primeros $n$ números naturales impares es $n^2$ .

Ejemplo #2

Problema. Sea $F_1=F_2=1$ y $F_n=F_{n-1}+F_{n-2}$ para $n \geq 3$ . La sucesión anterior es conocida como la sucesión de Fibonacci. Demuestre que:

$F_n = \dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^n-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\right)$ , para toda $n \in \mathbb{N}$ .

Sí, aunque no lo creas, hay una fórmula para calcular cualquier número de la sucesión de Fibonacci sin conocer los anteriores.

Solución. Usando inducción tenemos que:

Caso base: probemos que la proposición es cierta para $n=1$ y para $n=2$ . Por la definición tenemos que $F_1=F_2=1$ , y por la proposición tenemos que:

$F_1=\dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^1-\left(\dfrac{1-\sqrt{5}}{2}\right)^1\right)=\dfrac{1}{\sqrt{5}}\left(\dfrac{2\sqrt{5}}{2}\right)=1$

$F_2=\dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^2-\left(\dfrac{1-\sqrt{5}}{2}\right)^2\right)=\dfrac{1}{\sqrt{5}}\left(\dfrac{4\sqrt{5}}{4}\right)=1$

Por lo que la proposición es cierta para $n=1$ y $n=2$ .

Hipótesis de inducción: supongamos que la proposición se cumple para $n \geq 3$ , es decir, supongamos que $F_n = \dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^n-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\right)$ .
Tesis de inducción: probemos que la proposición es cierta para $n+1$ , es decir, probemos que $F_{n+1} = \dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^{n+1}-\left(\dfrac{1-\sqrt{5}}{2}\right)^{n+1}\right)$ . Al usar la definición de la sucesión tenemos que $F_{n+1}=F_n+F_{n-1}$ , pero por la hipótesis de inducción eso es:

$F_{n+1}=\dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^n-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\right)+\dfrac{1}{\sqrt{5}}\left(\left(\dfrac{1+\sqrt{5}}{2}\right)^{n-1}-\left(\dfrac{1-\sqrt{5}}{2}\right)^{n-1}\right)$

Factoricemos un poco para que se vea más sencilla la expresión:

$F_{n+1}=\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1+\sqrt{5}}{2}\right)^n\left(1+\left(\dfrac{1+\sqrt{5}}{2}\right)^{-1}\right)-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\left(1+\left(\dfrac{1-\sqrt{5}}{2}\right)^{-1}\right)\right]$

Pero $1+\left(\dfrac{1+\sqrt{5}}{2}\right)^{-1}=\dfrac{1+\sqrt{5}}{2}$ , y $1+\left(\dfrac{1-\sqrt{5}}{2}\right)^{-1}=\dfrac{1-\sqrt{5}}{2}$ , por lo tanto:

$F_{n+1}=\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1+\sqrt{5}}{2}\right)^n\left(\dfrac{1+\sqrt{5}}{2}\right)-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\left(\dfrac{1-\sqrt{5}}{2}\right)\right]$

$F_{n+1}=\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1+\sqrt{5}}{2}\right)^{n+1}-\left(\dfrac{1-\sqrt{5}}{2}\right)^{n+1}\right]$

Que es justo lo que queríamos demostrar, así, por inducción matemática, nuestra proposición es cierta para toda $n \in \mathbb{N}$ . $\quad \square$

Ejemplo #3

En ocasiones necesitamos aplicar la inducción matemática para demostrar alguna proposición que parece cierta para valores pequeños de $n$ , veamos cómo con el siguiente problema.

Problema. Sea $f : \mathbb{N} \to \mathbb{Q}$ tal que:

$f(1)=2017$
$\displaystyle \sum_{i=1}^{n} f(i)=n^2f(n)$ para $n \geq 2$

Halla el valor de $f(2017)$ .

Solución. Usemos de nuevo el truco de sacar el último término de la suma de la siguiente forma:

$\displaystyle \sum_{i=1}^{n-1} f(i)+f(n)=n^2f(n)$

Pero aguarda, el valor de $\displaystyle \sum_{i=1}^{n-1} f(i)$ es justamente $(n-1)^2f(n-1)$ por la definición de $f$ . Entonces tenemos:

$(n-1)^2f(n-1)+f(n)=n^2f(n)$

Ahora despejemos $f(n)$ en términos de $f(n-1)$ :

$f(n)=\dfrac{(n-1)^2f(n-1)}{n^2-1}=\dfrac{(n-1)^2f(n-1)}{(n+1)(n-1)}$

Podemos cancelar con toda seguridad el factor $(n-1)$ ya que recordemos que esta definición es para $n \geq 2$ , entonces:

$f(n)=\dfrac{n-1}{n+1}f(n-1)$

Hasta este punto tenemos una definición recursiva de $f$ , de tal forma que para calcular $f(n)$ solo necesitamos conocer $f(n-1)$ , calculemos algunos valores:

$f(2)=\dfrac{2-1}{2+1}f(2-1)=\dfrac{1}{3}f(1)$

$f(3)=\dfrac{3-1}{3+1}f(3-1)=\dfrac{2}{4}f(2)=\dfrac{1}{2} \cdot \dfrac{1}{3} f(1)=\dfrac{1}{6}f(1)$

$f(4)=\dfrac{4-1}{4+1}f(4-1)=\dfrac{3}{5}f(3)=\dfrac{3}{5} \cdot \dfrac{1}{6} f(1)=\dfrac{1}{10}f(1)$

$f(5)=\dfrac{5-1}{5+1}f(5-1)=\dfrac{4}{6}f(4)=\dfrac{2}{3} \cdot \dfrac{1}{10} f(1)=\dfrac{1}{15}f(1)$

Parece que la fórmula de $f$ es $f(n)=\dfrac{2}{n(n+1)}f(1)$ , demostrémoslo por inducción:

Caso base: Para $n=1$ tenemos que $f(1)=\dfrac{2}{1(1+1)}f(1)=f(1)$ , por lo que la fórmula es cierta para $n=1$ .
Hipótesis de inducción: Supongamos que $f(n)=\dfrac{2}{n(n+1)}f(1)$ .
Tesis de inducción. Probemos que $f(n+1)=\dfrac{2}{(n+1)((n+1)+1)}f(1)=\dfrac{2}{(n+1)(n+2)}f(1)$ . Por la definición recursiva tenemos que:

$f(n+1)=\dfrac{(n+1)-1}{(n+1)+1}f((n+1)-1)$

$f(n+1)=\dfrac{n}{n+2}f(n)$

Pero por la hipótesis de inducción:

$f(n+1)=\dfrac{n}{n+2} \cdot \dfrac{2}{n(n+1)}f(1)$

$f(n+1)=\dfrac{2}{(n+1)(n+2)}f(1)$

Por lo que tenemos que $f(n)=\dfrac{2}{n(n+1)}f(1)$ para todo $n \in \mathbb{N}$ . Finalmente, podemos decir con toda seguridad que $f(2017)=\dfrac{2}{2017(2017+1)}f(1)=\dfrac{2}{2017(2018)}(2017)=\dfrac{1}{1009}$ . $\quad \square$

Ahora estas listo mi joven padawan, ve y usa sabiamente esta poderosa arma. Suerte y que la fuerza te acompañe.

Anuncios

Aritmética Modular y Grupos Permutación

1 enero, 20179 marzo, 2017Oscar Rosas Deja un comentario

Congruencias

Clases Congruencia Módulo n

“ Las clases de congruencia modulo n son los conjuntos de enteros que tienen el mismo resto en la división entre n. ”

Los enteros se reparten entre pares e impares, pero también en vez de repartir los enteros según su residuo en la división entre 2, podemos repartirlos según su residuo en la división entre 3, entre 4 . . . entre cualquier entero n ≥ 2.

Por ejemplo, hay tres residuos posibles en la división entre 3, y los enteros se reparten según su residuo en los tres conjuntos siguientes:

Son los conjuntos de enteros que tienen el mismo resto en la división entre n. Si a es un entero, notamos su clase de congruencia módulo n.

Notación para el conjunto de las clases de congruencia modulo n

Sea n un entero. Notamos el conjunto de las clases de congruencia módulo n. Si n>0.

Congruencia Módulo n

De esta manera podemos definir la congruencia módulo n como:

a y b son congruentes módulo n si pertenecen a la misma clase de congruencia módulo n, es decir, si tienen el mismo resto en la división entre n.
Si n > 1. Dos enteros a y b son congruentes módulo n si y sólo si su diferencia es un múltiplo de n.

En regla general, si es un entero positivo, hay clases de congruencia módulo n, que son:

La clase es exactamente el conjunto de todos los enteros de la forma para .

Aritmética Modular

Sabemos que la suma de dos enteros pares siempre es par, la suma de dos enteros impares siempre es impar, y que la suma de un entero par y de un entero impar siempre es impar. Resumimos estas leyes de la manera siguiente:

El conjunto tiene tres elementos:

Si, por ejemplo, y entonces siempre se tiene y

Reglas Generales

Sea n en entero. Sean y dos clases módulo n.

Todas las sumas de un elemento de y de un elemento de están en una misma clase modulo n.

Todos los productos de un elemento de y de un elemento de están también en una misma clase modulo n.

Operaciones

Suma: A + B = (A+B) % n

Resta: A – B = (A-B) % n

Multiplicación: A * B = (A*B) % n

Función $\varphi$ de Euler

Teorema de Euler

Pequeño teorema de Fermat

Teorema Chino del residuo

Problemas diversos

Grupos Permutación

Estos grupos son algo muy importantes en Matemáticas:

Esta configuración inicial, la cual identificaremos como la permutación identidad I, usualmente se representa en los textos de matemáticas de la siguiente manera:

Relaciones y Funciones

1 enero, 201717 abril, 2017Oscar Rosas Deja un comentario

En álgebra y cálculo son importantes las relaciones entre variables; en geometría lo son las relaciones entre figuras.

Definición

Sean y conjuntos. Una relación de en es un subconjunto de , es decir:

Si , decimos simplemente que es una relación en .

Dominio y Contradominio

Dominio

Imagen – Contradominio

Relación Inversa

Reflexiva y Irreflexiva

Relación Reflexiva

» a tiene que estar relacionada con a, sin importar que a también está relaciona con otros elementos»

Relación Irreflexiva

Relación Identidad

Relación Cerradura Reflexiva

Es una relación que cumple con:

Simetría y Antisimetría

Simetría

Antisimetría

Relación Cerradura Simétrica

Es una relación que cumple con:

Transitividad

Si decimos que es transitiva entonces:

Relación Cerradura Transitiva

Es una relación que cumple con:

Funciones

Una función es una relación que cumple con las siguientes 2 condiciones:

“Todo los elementos del dominio tienen un valor asignado”

Para toda a que pertenece a A existe una b que pertenece a B es tal que:

“A cada valor del dominio solo le corresponde un único elemento del contradominio”

Si entonces

Gráficamente para que una relación sea función toda línea vertical debe tocar mínimo un punto de la gráfica y no más de un punto.

No son funciones

Es función

Tipos de Funciones

Funciones Continuas

Funciones incontables, y que pueden tomar cualquier valor como los Reales

Funciones Discretas Finitas

Funciones en las que solo pueden tomar valores selectos y son contables, como {1,34,1}

Funciones Discretas Infinitas

Funciones en las que solo pueden tomar valores selectos, pero son incontables, como los Naturales

Funciones Inyectivas

Funciones en las que solo le corresponde un elemento del conjunto A en el conjunto B. Una función es inyectiva si a cada valor del conjunto (dominio) le corresponde un valor distinto en el conjunto (imagen).

Es decir, a cada elemento del conjunto A le corresponde un solo valor tal que, en el conjunto A no puede haber dos o más elementos que tengan la misma imagen.

De forma gráfica: Si hay un punto en la función en el que pasa por dos puntos de una línea horizontal no es inyectiva.

Funciones Suprayectiva

Funciones en las que cada elemento del contradominio tiene un elemento en A. Una función es suprayectiva si está aplicada sobre todo el codominio, es decir, cuando la imagen , o en palabras más sencillas, cuando cada elemento de «Y» es la imagen de como mínimo un elemento de «X».

De forma gráfica: Si hay un punto en la función en el una línea horizontal no toque a la función no es suprayectiva.

Funciones Biyectiva

Funciones que son al mismo tiempo inyectivas y suprayectiva

…

* Tú, después de Relaciones y Funciones en Matemáticas Discretas*

Números Enteros

1 enero, 201712 febrero, 2017Oscar Rosas Deja un comentario

En esta lección me voy a centrar en los números enteros, pero antes de eso, creo apropiado hablarles de lo que hay más allá:

Naturales
Enteros
Racionales
Irracionales
Reales

Pero déjame los ordeno para ti, para que sea más fácil:

Reales: Conjunto que es la unión de los dos de abajo
- Racionales: Conjunto de números que se pueden expresar como una fracción
  - Enteros: Son un pequeño conjunto dentro de los racionales, que son lo que veremos
    - Naturales: Son los números enteros mayores a 0.
- Irracionales: Conjunto de números que NO se pueden expresar como una fracción.

Naturales

Los naturales son muy importantes para los matemáticos, si principal razón es que estos son la base de trabajo de la arma más poderosa de todos los matemáticos: La Inducción Matemática, da click y aprende de ella.

¿Los naturale incluyen el 0?

Eso siempre se me olvida, y después de preguntarles a varios matemáticos me dijeron que…NO.

Los Naturales Puros no incluyen el cero
Los Naturales Ampliados si que lo hacen

Esos tipos siempre tienen la respuesta a todo

Divisibilidad

Este concepto es algo difícil (al menos para mi) de comprender pero se puede sintetizar en que división de ambos pertenece a los números enteros, (ósea que es entero pues).

De manera formal, sean $a, b$ números enteros. Decimos que $a$ divide a $b$ si existe otro entero $q$ tal que $b=aq$ . La notación que usaremos para decir que $a$ divide a $b$ será $a \mid b$ . Algunas propiedades de la divisibilidad son:

Usualmente también decimos, para la notación $a \mid b$ , que $b$ es divisible entre $a$ , o que $b$ es múltiplo de $a$ .

Algoritmo de la división

Nosotros venimos dividiendo desde la primaria, en donde si queríamos dividir a $a$ entre $b$ , obteníamos un cociente (llamémosle $q$ ) y residuo (llamémosle $r$ ). Pues de manera algebráica, estos cuatro números cumplen con la relación $a=bq+r$ , donde $0 \leq r < \lvert b \rvert$ .

Vemos que la primera relación, básicamente nos dice cuántas veces cabe $b$ en $a$ sin pasarse y, para que se cumpla esto último, requerimos que el residuo $r$ sea un entero menor a $\lvert b \rvert$ pero mayor o igual a cero, de ahí la segunda relación.

Resulta evidente (pero esto no es obvio, se demuestra por inducción), que para cualesquiera $a,b \in \mathbb{Z}$ con $b \neq 0$ existen $q,r \in \mathbb{Z}$ únicos que cumplen con lo anterior.

Ejemplo. Efectúa la división de 47 entre 6. Vemos que el 6 cabe 7 veces en el 47 sin pasarse y sobran 5. Entonces, $47=6 \times 7+5$ , así $q=7$ y $r=5$ .

Cuando tenemos que efectuar la división con números negativos, tenemos que cuidar que ambas condiciones se sigan cumpliendo, en especial la de $0 \leq r < \lvert b \rvert$ .

Números primos

Decimos que un $p \in \mathbb{Z}$ es primo si:

$p > 1$ .
Sea $q \in \mathbb{N}$ . Si $q \mid p$ , entonces $q=1$ o $q=p$ .

Es decir, todos los números primos son mayores o iguales a 2 y solo los naturales $1$ y $p$ dividen a $p$ .

Sean $a,b \in \mathbb{Z}$ . Decimos que $a$ y $b$ son primos relativos si no existe un $p \in \mathbb{Z}$ primo tal que $p \mid a$ y $p \mid b$ .

Máximo Común Divisor

Este concepto es algo intuitivo, ya que se refiere al máximo numero natural que sea capaz de dividir a otros dos números enteros $a$ y $b$ . Pero ni modo, también tenemos que formalizar lo anterior y queda así:

Sean $a, b \in \mathbb{Z}$ . Decimos que $d \in \mathbb{Z}$ es el máximo común divisor de $a$ y $b$ si:

$d > 0$ .
$d \mid a$ y $d \mid b$ .
Sea $q \in \mathbb{Z}$ tal que $q \mid a$ y $q \mid b$ , entonces $q \mid d$ .

Usaremos la notación $d=(a,b)$ .

Ok, vayamos por partes entendiendo cada punto de la definición:

El primero es sencillo, quien quiera ser el máximo común divisor de $a$ y $b$ tiene que ser entero positivo, o natural simplemente. Digamos que nuestro candidato es $d$ .
Luego, obviamente, $d$ también tiene que dividir a $a$ y a $b$ , ¿si no por qué se llamaría común?
Finalmente, si llega algún otro entero $q$ que dice ser el máximo común divisor de $a$ y $b$ , tenemos que $q$ tiene que dividir a $d$ ; esto nos garantiza que $d$ sea en efecto el máximo común divisor.

Tenemos las siguientes propiedades, donde $a,b,c,p,q,r \in \mathbb{Z}$ y $p$ es primo:

Por convención, asumamos que $(0,0)$ es una indeterminación, para ahorrarnos problemas.
$(a,b)=(b,a)=(-a,b)$
Si $a \mid b$ , entonces $(a,b)=\lvert a \rvert$ .
Si $a \neq 0$ , entonces $(a,0)=|a|$ .
Si $a=bq+r$ , entonces $(a,b)=(b,r)$ .
$(ac,bc)=\lvert c \rvert (a,b)$
Si $a \mid bc$ y $(a,b)=1$ , entonces $a \mid c$
$(a, a+1)=1$
$p \mid a$ o $(a,p)=1$
Si $p \mid ab$ , entonces $p \mid a$ o $p \mid b$
$a$ y $b$ son primos relativos si y solo si $(a,b)=1$

Pero te preguntarás, ¿cómo puedo calcular $(a,b)$ de manera rápida, sin tener que recurrir al tanteo?

Algoritmo de Euclides

Sí, Euclides contribuyó también en teoría de números aparte de geometría. Sean $a,b \in \mathbb{Z}$ no ambos cero. Su algoritmo sirve para calcular $(a,b)$ con una repetida aplicación del algoritmo de la división.

Usaremos la quinta propiedad de la lista anterior, escogiendo $q$ y $r$ mediante el algoritmo de la división. Sin pérdida de generalidad asumamos que $a,b \geq 0$ y que $a \geq b$ . Debido a que $(a,b)=(b,r)$ y que $0 \leq r < b$ , usaremos recursividad para llegar a un punto en que tengamos que calcular algo como $(x,0)$ , y eso es igual a $x$ . Veamos cómo:

Comencemos asignando $r_0 \gets a$ , $r_1 \gets b$ y $i \gets 2$ .
Mientras :
- Sea esta la $i$ -ésima iteración.
- Efectuemos el algoritmo de la división para dividir $r_{i-2}$ entre $r_{i-1}$ , es decir, hallemos $q_i, r_i \in \mathbb{Z}$ tales que $r_{i-2}=r_{i-1}q_i+r_i$ con $0 \leq r_i < r_{i-1}$ .
- Aumentemos $i$ en $1$ (solo para llevar el orden del algoritmo).
Tenemos que $(a,b)=r_{i-2}$ .

Veamos un ejemplo:

Problema. Halla el máximo común divisor de $240$ y $46$ .

Solución. Comencemos asignando los residuos iniciales: $r_0=240$ y $r_1=46$ . Entonces:

$240=46 \times 5+10\\ 46=10 \times 4+6\\ 10=6 \times 1+4\\ 6=4 \times 1+2\\ 4=\boxed{2} \times 2+0$

Por lo tanto, $(240, 46)=2$ . Vemos que la secuencia de residuos que obtuvimos fue: $240, 46, 10, 6, 4, 2, 0$ ; y que el valor de $(240,46)$ es el último residuo distinto de cero.

Identidad de Bézout

Sean $a,b \in \mathbb{Z}$ no ambos cero, entonces existen $s,t \in \mathbb{Z}$ tales que $sa+tb=(a,b)$ . Es decir, existe una combinación lineal de $a$ y $b$ tal que es igual a su máximo común divisor.

Esta identidad es muy poderosa, ya que nos permite demostrar muchas proposiciones que involucran divisibilidad y máximo común divisor. Por ejemplo, tenemos el teorema que afirma que si existen $s, t \in \mathbb{Z}$ tales que $sa+tb=1$ , entonces $(a,b)=1$ .

Algoritmo extendido de Euclides

Este algoritmo nos sirve para hallar $s,t \in \mathbb{Z}$ que satisfagan la identidad de Bézout, además del mínimo común múltiplo de $a$ y $b$ . Vamos a proceder con base en el Algoritmo de Euclides, pero agregando unos pasos extra:

Comencemos asignando $r_0 \gets a$ , $r_1 \gets b$ , $s_0 \gets 1$ , $t_0 \gets 0$ , $s_1 \gets 0$ , $t_1 \gets 1$ y $i \gets 2$ .
Mientras :
- Sea esta la $i$ -ésima iteración.
- Efectuemos el algoritmo de la división para dividir $r_{i-2}$ entre $r_{i-1}$ , es decir, hallemos $q_i, r_i \in \mathbb{Z}$ tales que $r_{i-2}=r_{i-1}q_i+r_i$ con $0 \leq r_i < r_{i-1}$ .
- Asignemos $s_i \gets s_{i-2}-s_{i-1}q_i$ y $t_i \gets t_{i-2}-t_{i-1}q_i$
- Aumentemos $i$ en $1$ (solo para llevar el orden del algoritmo).
Tenemos que $s_{i-2}a+t_{i-2}b=r_{i-2}=(a,b)$ .

Tomemos de nuevo el ejemplo anterior, pero esta vez llevando los valores en una tabla:

$\begin{array}{|c|c|c|c|c|c|} \hline \text{Iteracion } (i) & \text{Algoritmo de la division} & q_i & r_i & s_i & t_i \\ \hline 0 & & & 240 & 1 & 0 \\ \hline 1 & & & 46 & 0 & 1 \\ \hline 2 & 240 = 46 \times 5 + 10 & 5 & 10 & 1 - 0 \times 5 = 1 & 0 - 1 \times 5 = -5 \\ \hline 3 & 46 = 10 \times 4 + 6 & 4 & 6 & 0 - 1 \times 4 = -4 & 1 - (-5) \times 4 = 21 \\ \hline 4 & 10 = 6 \times 1 + 4 & 1 & 4 & 1 - (-4) \times 1 = 5 & -5 - 21 \times 1 = -26 \\ \hline 5 & 6 = 4 \times 1 + 2 & 1 & 2 & -4 - 5 \times 1 = -9 & 21 - (-26) \times 1 = 47 \\ \hline 6 & 4 = 2 \times 2 + 0 & 2 & 0 & 5 - (-9) \times 2 = 23 & -26 - 47 \times 2 = -120 \\ \hline 7 & & & & & \\ \hline \end{array}$

Por lo tanto, $(-9)(240)+(47)(46)=2$ . De hecho nos pudimos haber ahorrado calcular $s_6$ y $t_6$ en la sexta iteración, ya que el residuo obtenido ahí ( $r_6$ ) es $0$ y con eso terminamos. Sin embargo, resulta que $\dfrac{a}{b}=-\dfrac{t_{i-1}}{s_{i-1}}$ , donde la fracción $\dfrac{t_{i-1}}{s_{i-1}}$ está en su mínima expresión. En este caso, $\dfrac{240}{46}=\dfrac{120}{23}$ . Otra utilidad más de este algoritmo, qué impresionante.

Ahora analicemos por qué funciona este poderoso algoritmo:

Básicamente primero aplicamos el algoritmo normal, y una vez que terminemos, vamos despejando los residuos de cada ecuación de tal forma que siempre queden como combinación lineal de $a$ y $b$ . Tomando el ejemplo de $a=240$ y $b=46$ tenemos que:

$240=46 \times 5+10 \Longrightarrow 10=(1)(240)+(-5)(46)$

$46=10 \times 4+6 \Longrightarrow 6=46-4(10)=46-4[(1)(240)+(-5)(46)]=(-4)(240)+(21)(46)$

$10=6 \times 1+4 \Longrightarrow 4=10-1(6)=[(1)(240)+(-5)(46)]-[(-4)(240)+(21)(46)]=(5)(240)+(-26)(46)$

$6=4 \times 1+2 \Longrightarrow 2=6-1(4)=[(-4)(240)+(21)(46)]-[(5)(240)+(-26)(46)]=(-9)(240)+(47)(46)$

De manera general, en cada iteración comenzando con $i=2$ queremos expresar $r_i$ como combinación lineal de $a$ y de $b$ , es decir, $r_i=s_i a+t_i b$ con $s_i, t_i \in \mathbb{Z}$ . Pero por definición de $r_i$ tenemos que $r_i=r_{i-2}-r_{i-1}q_i$ . Combinando ambas ecuaciones llegamos a:

$r_i=s_{i-2}a+t_{i-2}b-(s_{i-1}a+t_{i-1}b)q_i=(s_{i-2}-s_{i-1}q_i)a+(t_{i-2}-t_{i-1}q_i)b$

Por lo tanto, $s_i=s_{i-2}-s_{i-1}q_i$ y $t_i=t_{i-2}-t_{i-1}q_i$ . Ahora tenemos que hallar los valores iniciales de $s$ y $t$ , es decir, $s_0,t_0,s_1,t_1$ . Tenemos que:

$a=r_0=s_0 a+t_0 b \Longrightarrow s_0=1, t_0=0$

$b=r_1=s_1 a+t_1 b \Longrightarrow s_1=0, t_1=1$

Finalmente, supongamos que en la $i$ -ésima iteración tenemos $r_{i-1}=0$ . Como tenemos que dividir $r_{i-2}$ entre $r_{i-1}$ y no podemos dividir entre cero, nos detenemos ahí y vemos que:

$(a,b)=(r_0,r_1)=(r_1,r_2)=\cdots=(r_{i-2},r_{i-1})=(r_{i-2},0)=r_{i-2}=s_{i-2}a+t_{i-2}b$

Tenemos garantizado que este algoritmo siempre terminará, ya que la secuencia de los residuos es decreciente y en alguna iteración tendremos que $r_{i-1}=0$ , ya que por el algoritmo de la división, $0 \leq r_i < r_{i-1}$ para $i \geq 2$ , y generalizando a todos los residuos, $r_1 > r_2 > \cdots >r_{i-1}=0$ .

Ecuaciones diofánticas

Resulta que los enteros $s,t \in \mathbb{Z}$ que satisfacen la identidad de Bézout no son únicos, por ejemplo, tomando el caso de $240$ y $46$ también tenemos que $(14)(240)+(-73)(46)=2$ .

Supongamos que queremos hallar las soluciones enteras de la ecuación $ax+by=c$ , donde $a,b,c \in \mathbb{Z}$ . Esta ecuación tendrá soluciones enteras si y solo si $(a,b)|c$ .

Para ver que $(a,b)|c$ implica que la ecuación tenga soluciones enteras; vemos que existen $s,t \in \mathbb{Z}$ tales que $sa+tb=(a,b)$ , pero también $c=(a,b)k$ para alguna $k \in \mathbb{Z}$ , entonces $sak+tbk=(a,b)k=c$ , por lo que claramente una solución será $x=sk$ y $y=tk$ , donde $k=\dfrac{c}{(a,b)}$ .

Para ver que el hecho de que la ecuación tenga soluciones enteras implica que $(a,b)|c$ ; supongamos que la solución es $x=x_0$ y $y=y_0$ , así $ax_0+by_0=c$ . Pero $(a,b)|a$ y $(a,b)|b$ , entonces $(a,b)$ dividirá a cualquier combinación lineal de $a$ y $b$ , y qué mejor que divida justamente a $ax_0+by_0$ , así $(a,b)|ax_0+by_0$ , por lo tanto $(a,b)|c$ .

Veamos muchos ejemplos de lo anterior:

Problema. Determina si la ecuación $4x+10y=6$ tiene soluciones enteras, y en caso de tenerlas, halla una.

Solución. Al efectuar el algoritmo extendido de Euclides con $a=4$ y $b=10$ tenemos que $(4,10)=2=(-2)(4)+(1)(10)$ . En esta ecuación $c=6$ , y como $(4,10)|6$ , la ecuación sí tiene soluciones enteras. Tenemos que $s=-2$ , $t=1$ y $k=\dfrac{6}{(4,10)}=3$ , por lo que una solución será $x=(-2)(3)=-6$ y $y=(1)(3)=3$ .

Problema. Determina si la ecuación $6x+15y=7$ tiene soluciones enteras, y en caso de tenerlas, halla una.

Solución. Al efectuar el algoritmo extendido de Euclides con $a=6$ y $b=15$ tenemos que $(6,15)=3=(3)(6)+(-1)(15)$ . En esta ecuación $c=7$ , y como $(6,15) \nmid 7$ , la ecuación no tiene soluciones enteras.

Ahora, determinemos la estructura de las soluciones de este tipo de ecuaciones. Sea $x_0$ y $y_0$ una solución de la ecuación $ax+by=c$ , entonces $x=x_0+\dfrac{b}{(a,b)}k$ y $y=y_0-\dfrac{a}{(a,b)}k$ forman la familia de soluciones de la ecuación para toda $k \in \mathbb{Z}$ .

Para comprobar que esas son soluciones, basta con sustituirlas y ver que satistagan la ecuación:

$a\left(x_0+\dfrac{b}{(a,b)}k\right)+b\left(y_0-\dfrac{a}{(a,b)}k\right)=\\ax_0+\dfrac{ab}{(a,b)}k+by_0-\dfrac{ab}{(a,b)}k=ax_0+by_0=c$

(por la suposición de que $x_0$ y $y_0$ es una solución).

Por último, para demostrar que las soluciones anteriores en realidad nos dan todas las soluciones, supongamos que tenemos otra solución $(x,y)$ además de la inicial $(x_0,y_0)$ , entonces:

$ax+by=c \\ ax_0+by_0=c$

Restando obtenemos que:

$a(x-x_0)+b(y-y_0)=0 \Longrightarrow a(x-x_0)=b(y_0-y)$

Dividiendo entre $(a,b)$ obtenemos:

$\dfrac{a}{(a,b)}(x-x_0)=\dfrac{b}{(a,b)}(y_0-y)$

Vemos que $\dfrac{b}{(a,b)} \bigm| \dfrac{a}{(a,b)}(x-x_0)$ , pero como $\dfrac{b}{(a,b)}$ y $\dfrac{a}{(a,b)}$ son primos relativos, entonces $\dfrac{b}{(a,b)} \mid (x-x_0)$ , por lo que existe $k \in \mathbb{Z}$ tal que $x-x_0=\dfrac{b}{(a,b)}k$ , así $x=x_0+\dfrac{b}{(a,b)}k$ . Finalmente obtengamos $y$ al sustituir en la ecuación inicial:

$a(x-x_0)=b(y_0-y) \\ \dfrac{ab}{(a,b)}k=b(y_0-y) \\ \dfrac{a}{(a,b)}k=y_0-y \\ y=y_0-\dfrac{a}{(a,b)}k$

Ejemplo: retomando la ecuación $4x+10y=6$ , obtuvimos una solución inicial $(x_0,y_0)=(-6,3)$ , por lo tanto, la estructura de sus soluciones será:

$x=-6+\dfrac{10}{2}k=-6+5k$

$y=3-\dfrac{4}{2}k=3-2k$

$(x,y)=(-6+5k, 3-2k)$

Si tomamos $k \in \{0,1,2,3\}$ , obtendríamos las soluciones $(x,y)=(-6,3),(-1,1),(4,-1),(9,-3)$ .

Sistemas de numeración

Seguramente recordarás en cursos anteriores que descomponías un número en unidades, decenas, centenas, etc. Por ejemplo, en el número 468 tenemos 8 unidades, 6 decenas y 4 centenas. Igual recuerdas que el valor de un dígito depende de su posición, de hecho esta es la característica principal de los sistemas de numeración posicionales: el número 8 vale 8, el 6 vale 60 y el 4 vale 400; en efecto, 8+60+400=468.

De manera general, tomando un $x \in \mathbb{N}$ , podemos representarlo mediante sus $n+1$ dígitos en base 10 de la siguiente forma:

$\displaystyle x=\sum_{k=0}^{n} a_k {10}^k$

Donde todos los $a_k$ son dígitos, es decir, $0 \leq a_k < 10$ y $a_n \neq 0$ . Por ejemplo, $468=8 \cdot 10^0+6 \cdot 10^1+4 \cdot 10^2$ , por lo que $a_0=8$ , $a_1=6$ y $a_2=4$ .

Sin embargo, la definición anterior nos permite generalizar e introducir el concepto de un número $x$ de $n+1$ dígitos expresado en base $b$ , donde $b \geq 2$ y $0 \leq a_k < b$ :

$\displaystyle x=\sum_{k=0}^{n} a_k b^k$

Para identificar que $x$ está en base $b$ , escribiremos $x_b$ , excepto cuando $b=10$ , en donde simplemente escribiremos $x$ .

Ejemplo. Halla el valor de $13402_5$ en base 10.

Solución. Usando la definición tenemos que:

$\displaystyle 13402_5 = \sum_{k=0}^{4} a_k 5^k \\ =2 \cdot 5^0+0 \cdot 5^1+4 \cdot 5^2+3 \cdot 5^3+1 \cdot 5^4\\ =2+0+100+375+625=1102$

Al usar bases mayores a 10, usaremos las letras del abecedario. Por ejemplo, el conjunto de los dígitos en base 16 es $\{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}$ , donde $A=10$ , $B=11$ y así sucesivamente.

Ahora, veamos cómo convertir un número $x \in \mathbb{N}$ en base 10 a cualquier base $b$ :

Asignamos $x_0 \gets x$ y $i \gets 0$ (solo para llevar el orden de las iteraciones).
Sea esta la $i$ -ésima iteración. Mediante el algoritmo de la división dividimos $x_i$ entre $b$ , es decir, obtenemos $x_{i+1},r_i$ tales que $x_i=bx_{i+1}+r_i$ con $0 \leq r_i < b$ .
Si $x_{i+1}=0$ vamos al paso 4, si no, asignamos $i \gets i+1$ y vamos al paso 2.
Tenemos que $\displaystyle x=\sum_{k=0}^{i} r_k b^k=\overline{r_i r_{i-1} \ldots r_1 r_0}_b$ . Es decir, concatenamos los residuos del último al primero para formar la representación en base $b$ de $x$ .

Ejemplo. Convierte el número $16539$ a base 7.

Solución. Tenemos que:

$16539 = 7 \times 2362 + 5$
$2362 = 7 \times 337 + 3$
$337 = 7 \times 48 + 1$
$48 = 7 \times 6 + 6$
$6 = 7 \times 0 + 6$

Por lo tanto, $16539 = 66135_7$ .

Para convertir un número $x$ de base $b$ a base $c$ , primero convertimos $x_b$ a base 10 y luego a base $c$ . Veamos cómo:

Ejemplo. Convierte el número $34215_6$ a base $13$ .

Solución. Primero convirtamos $34215_6$ a base 10. Tenemos que:

$\displaystyle 34215_6 = \sum_{k=0}^{4}a_k 6^k \\ =5 \cdot 6^0+1 \cdot 6^1+2 \cdot 6^2+4 \cdot 6^3+3 \cdot 6^4\\ =5+6+72+864+3888=4835$

Luego, convirtamos $4835$ a base 13, tenemos que:

$4835 = 13 \times 371 + 12$
$371 = 13 \times 28 + 7$
$28 = 13 \times 2 + 2$
$2 = 13 \times 0 + 2$

Por lo tanto, $34215_6=227C_{13}$ .

Conjuntos

30 diciembre, 20168 julio, 2017Oscar Rosas Deja un comentario

Si quieres la versión hardcore tienes que dar click

¿Qué son?

Olvida todo lo que sabes sobre números. Olvídate de que sabes lo que es un número. Aquí es donde empiezan las matemáticas. En vez de matemáticas con números, vamos a hacer matemáticas con ’cosas’.

Se denomina conjunto a la agrupación de entes o elementos, que poseen una o varias características en común.

Un conjunto puede ser una agrupación de números, de vectores, de autos, de espacios vectoriales, de objectos, de funciones e incluso un conjunto puede ser una agrupación de otros conjuntos.

¿Cómo Definirlo?

Pertenecia

Creo que el símbolo más importante al hablar de conjuntos es este: x ∈ A. Esto quiere decir, el elemento x pertenece al Conjunto A.

Forma Básica

Recuerda también que:

Notación Formal

Esta notación tiene un nombre genial en inglés, se le conoce como Set Builder Notation, esta notación es la que sueles encontrar en los libros.

Se ve fea al principio pero te da toda la información que necesitas.

Definimos cierto conjunto, al que llamaremos A como la agrupación de todas las x (es decir cada x es un elemento, un ente) tal que cumplen ciertas características.

Clasificación de Conjuntos

Los conjuntos pueden clasificarse en función de su número de elementos, en:

Finito: Si tiene una colección que se pueda contar, aunque sea difícil. Por ejemplo, el conjunto de frutas incluye todos los tipos de fruta que hay en el mundo. Aunque sea difícil, se podrían contar todos los tipos de fruta del mundo, por lo que es finito.
Infinito: Si tiene una colección que no se pueda terminar de contar nunca. Por ejemplo, el conjunto de todos los números pares, que son infinitos, es un conjunto infinito.

Conjunto Vacío: φ

Ok, ya sabemos que un conjunto es un grupo de elementos, pero … ¿Cómo represento a un conjunto en el que no hay nada?

Como una caja vacía.

De hecho, me gusta, hablemos de el Conjunto vacío como un caja vacía.

Llamemos φ como aquel conjunto tal que φ = {} es decir el conjunto que no tiene elementos.

Listo, eso es casí todo, además te gustará que te recuerde las siguientes proposiciones:

|φ| = 0 : Esto quiere decir que la cardinalidad (es decir la cantidad de elementos) del conjunto vacío es la misma que la cantidad de galletas en una caja vacía de galletas, osea 0.

φ ̸= {φ} : Esto quiere decir que no es lo mismo hablar del conjunto vacío que de hablar de un conjunto cualquiera que contiene al conjunto vacío.

Es decir simplemente no es lo mismo tener una caja vacía que una caja con una caja vacía dentro (si lo piensas la segunda caja ya no esta completamente vacía).

Conjunto Universo: U

Como podemos imaginarnos, tenía que existir un término inverso, digamos que estamos analizando y agrupando animales por su habitad, entonces tenemos muchos conjuntos cool como animales del bosque o marinos, pero también tenemos a un mega conjunto que llamamos universo donde tenemos a todos los animales.

Muchas veces a la hora de hablar sobre conjuntos solemos definirlos sobre un universo.

Subconjuntos A ⊆ B

Esta es la relación mas importante siento yo, porque será la que mas ocupemos a lo largo del tiempo.

Que el A sea un subconjunto de B quiere decir que todos los elementos de A también son elementos de B.

Subconjuntos Propios
A es un subconjunto propio de B si y sólo si cada elemento de A está en B, y existe por lo menos un elemento de B que no está en A.

Operaciones

Podemos hacer operaciones con los conjuntos de una manera muy similiar a como hacemos operaciones con los números normales, tu defines una operación, y la haces entre dos conjuntos y esta te dará un nuevo conjunto, pero aquí siento que son incluso más divertidas.

Intersección

Esta operación básicamente nos da un conjunto en el que estan solo los elementos que bien pertenezcan a A y que también pertenezcan a B.

Unión

Esta operación basicamente nos da un conjunto en el que estan todos los elementos que bien pertenezcan a A o bien que pertenezcan a B.

Resta

Esta operación basicamente nos da un conjunto en el que estan todos los elementos de A que no pertenezcen a B.

A esta operación también se la conoce como complemento relativo.

Complemento

Esta operación basicamente nos da un conjunto en el que estan todos los elementos que no pertenecen a A.

Diferencia Simétrica

Esta operación basicamente nos da un conjunto en el que estan todos los elementos que pertenezcen a A y a B, pero no a ambos.

Otra forma de definirlo es:

Producto Cartesiano

Esta es la base de lo que se conoce como es plano cartesiano, y es quizá la operación mas útil que vas a conocer a lo largo de estos textos, veamos específicamente porque:

N-Tuplas

El resultado de un producto cartesiano es un con- junto formado de n-tuplas, cada n-tuplas es una agrupación ordenada de elementos. Por ejemplo (a,b) ó (x,y,z).

Esta operación basicamente nos da un conjunto en el que estan todas las n-tuplas donde su primer elemento pertenece a A y su segundo elemento pertenece a B.

Ideas Importantes

Tabla

Podemos hacer uso de una tabla para encontrar todos los elementos del producto cartesiano.

Conjunto Potencia

El conjunto que contiene a todos los subconjuntos posibles.

Esta operación es diferente en el sentido de que no toma sus elementos del conjunto que toma como entrada, sino que usa esos elementos para combinarlos y crear subconjuntos que son los elementos de esta nueva operación.

Ok, ok, quizá me puse muy intenso con el párrafo de arriba, veamos un poco más calmado como es que funciona.

Esta operación basicamente nos da un conjunto en el que estan todos los conjuntos que son sub- conjuntos de tu conjunto original.

Ideas Importantes

Tabla

Podemos hacer uso de una tabla y el binario para encontrar todos los elementos del conjunto potencia.

Si quieres crear un conjunto potencia, escribe la sucesión de números binarios de n cifras, y con cada número haz un subconjunto: Cuando haya un ′1′, añade el elemento que corresponde.

Leyes del Álgebra de Conjuntos

Cardinalidad

Ok, vamos avanzando, ahora es la hora de ver una característica de los conjuntos. La Cardinalidad, que no es mas que una forma fancy de decir el número de elementos ó entes que contiene cierto conjunto.

Puedes verlo como una función que recibe un conjunto cualquiera y te regresa un número (Bueno, tecnicamente también sta el caso en el que la cardinalidad es infinita).

Esta es la forma en que solemos expresar la car- dinalidad de un conjunto cualquiera:

Cosas Utiles

Lógica

30 diciembre, 201610 agosto, 2017Oscar Rosas Deja un comentario

Proposiciones

La lógica es una forma sistemática de pensar que nos permite deducir nueva información desde la información que ya conocemos.

Recuerda que la lógica es un proceso de deducir la información correctamente, no sólo deducir la información correcta.

La lógica trabajo con algo llamado proposiciones, son como las funciones para cálculo, o los lenguajes de programación para informática o los libros para la literatura.

Así que empecemos por ahí … ¿Qué son?

Son proposiciones las frases que pueden adquirir un valor de verdadero o falso.

O dicho de manera formal: Es una oración aseverativa de la que tiene sentido decir que es verdadera o falsa.

Y cuando digo frase, me refiero a:

Secuencia finita de signos con significado y sentido de ser calificado como verda- dero o falso. (es decir una simple expresión matemática).

Expresión lingüística susceptible de ser calificada de verdadera o falsa. (es decir una frase aseverativa).

Sentencias Abiertas

Existen cosas que son parecidas a las proposiciones, pero no lo son exactamente, son cosas como:

p(x): x es un número par.

Puesto que la validez de p(x) depende que número sea x, p(x)no es no totalmente cierta ni totalmente falsa, por lo tanto no es una proposición.

Una oración como esta, cuya verdad depende del valor de una o más variables, se llama sentencias abierta.

Ejemplo:

Por ejemplo son proposiciones frases como:

2+3=4
Hay solamente 325 personas en Marte
∀x,y ∈ N se tiene que x+y ∈ R
Hoy es lunes
f(x + y) = f(x) + f(y)
Si x = 2 entonces 2x = 4

Pero no son cosas como:

¡Ojalá no llueva hoy! Haz la tarea
Este enunciado es falso Tomar una siesta

Teoremas, Corolarios y Tautologías

Propiedades de una Proposición:

Tautología: Cuando para todos los valores posibles de un conjunto de proposiciones siempre será verdadero el conjunto.
Contradicción: Cuando para todos los valores posibles de un conjunto de proposiciones esta será siempre falso.
Contingencia: Una proposición «común» son básicamente todas las que no son ni tautologías ni contradicciones.

Notación

Además a los matemáticas les encanta demostrar todo y cuando digo todo, es TODO, así que aquí te dejo las diferencias entre varias palabras que se parecen:

Proposición: Enunciado que encierra un valor de verdad

Axioma: Principio tan claro y evidente que no necesita demostración.
Corolario: Proposición demostrado que provoca una afirmación.
Demostración: Razonamiento por el cuál se da prueba de la exactitud de una proposición.
Lema: Proposición que es necesaria demostrar antes de establecer un teorema.

Conectores Lógicos

Conector		Formas Equivalentes	Símbolo
y	p y q	Conjunción de p y de q.	p ∧ q
o	p o q	Disyunción de p y de q.	p ∨ q
no	no p	Negación de p.	¬p
implica	p implica q	Si p, entonces q p implica qq si p p sólo si q Cuando p, q q siempre que p Siempre que q, p p es suficiente para q q es necesaria para p p es una condición suficiente para q q es una condición necesaria para pEs necesario que q para p Sólo si q entonces p Es suficiente que p para que q	p → q
si y sólo si	p si y sólo si q	p ssi q. p es equivalente a q Bicondicional.	p ↔ q

Tabla de Verdad

Jerarquía de los Exponentes

Como en todas las matemáticas, no todos los operadores tiene el mismo «poder», así que se los escribo, del mas poderoso (el que tendrás que hacer primero) al más débil (el que harás al final).

Leyes de la Lógica

Aquí v es una tautología (cualquiera), y f es una contradicción (cualquiera).

Condicionales

Equivalencia

Es cuando dos conjuntos de Proposiciones es lógicamente igual, y se escribe como:

Es decir que si se hace la bicondicional entre estos dos conjuntos de proposiciones será una tautología.

Contraejemplo: Cuando se demuestra que un enunciado es falso dando ejemplo de los casos en los que no se cumple.

Demostraciones Indirectas

Inferencia Lógica

La inferencia es la forma en la que obtenemos conclusiones en base a datos y declaraciones establecidas.

Podemos entonces definir que una inferencia lógica es un proposición q que si le aplicamos el condicional con la disyunción de todas las premisas sería una tautología.

Propiedades

Reglas de Inferencia

Cuantificadores

Los cuantificadores permiten la construcción de proposiciones a partir de funciones proposicionales, bien sea particularizando o generalizando.

Así, un cuantificador transforma una función proposicional, en una proposición a la cual se le asigna un valor de verdad.

Leyes de Distribución de los Cuantificadores

…

Vaya eso fue intenso, lo siento si me pase con la teoría, pero espero que les sirva par poder lograr todo lo que les falte, suerte amigos…

O quizá quieras más, si es así, vamos la siguiente lección te esta esperando.

Memoria Dinámica

24 diciembre, 201628 diciembre, 2016Oscar Rosas Deja un comentario

Tipos de Memoria

La memoria Estética

Sin importa nada, ocupa todo el espacio de las variables que declaramos, no le importa si las usamos.

Memoria Dinámica

Puede hacerse más más compleja y dar muchos errores.
Da la capacidad de modificar tamaño de variables.
SIEMPRE se usan punteros.
Es mucho más lento un programa que la implemente pues ocupa más instrucciones.

Funciones de Memoria Dinámica

Para poder usarla hay que añadir a librería

Malloc

Esta función sirve para reservar un espacio de memoria tan grande como se especifica dentro de la función.

La función malloc() y en general, cualquier función de reserva dinámica de memoria, devuelve un puntero nulo (NULL) si la reserva de memoria no puede realizarse, generalmente por falta de memoria disponible.

Por ello, antes de usar un puntero devuelto por la función malloc() es imprescindible comprobar que dicho puntero no es nulo (NULL).

Calloc

Esta función sirve para reservar un espacio de memoria tan grande como se especifica dentro de la función y al mismo tiempo inicializa todos a 0.

Es mucho más lento que Malloc.

Realloc

Redimensiona un tipo de dato que asignamos con Malloc pero conservando sus valores.

Free

La memoria dinámica reservada es eliminada siempre al terminar la ejecución del programa por el propio sistema operativo. Sin embargo, durante la ejecución del programa puede ser interesante, e incluso necesario, proceder a liberar parte de la memoria reservada con anterioridad y que ya ha dejado de ser necesario tener reservada.

Esto puede realizarse mediante la función free(). La función free() tiene la forma:

void free(void *p);

Donde p es la variable de tipo puntero cuya zona de memoria asignada de forma dinámica queremos liberar.

Vectores Dinámicos

Declararlo

tipo *NombreArray;

Donde:

tipo Es un tipo de dato (int, char)

Asignarle un tamaño al Vector(Malloc)

NombreDelVector = (tipo*)malloc( Tamaño*sizeof(tipo) );

Donde:

Tamaño Es el número de posiciones que tendrá nuestro vector.
Tipo Es un tipo de dato (int, char)

Aquí unos ejemplos:

// == EJEMPLO 1 ==
//Declararlo
int *Vector1;

//Ponerle tamaño al Vector
Vector1 = (int*)malloc(50*sizeof(int));

// == EJEMPLO 2 ==

//Declararlo
double **Vector2;

//Ponerle tamaño al Vector
*Vector2 = (double**)malloc(70*sizeof(double*));

Asignarle un tamaño al Vector(Calloc)

NombreDelVector = (tipo*)calloc( Tamaño*sizeof(tipo) );

Donde:

Tamaño Es el número de posiciones que tendrá nuestro vector.
Tipo Es un tipo de dato (int, char)

Modificar el tamaño del Vector

NombreDelVector = (tipo*)realloc( NombreDelVector, NuevoTamaño*sizeof(tipo) );

Strings Dinámicos

Para trabajar con ellos es mucho más sencillo genera un string estático y en el meter los valores iniciales y ya luego pasarle los valores al string dinámico que los conservara.

Declararlo

char NombreDelString;    //Vector Real
char StringAux;          //Vector Auxiliar

Asignarle un tamaño al Vector(Malloc)

NombreDelString = (char*)malloc((strlen(StringAux)+1)*sizeof(char));

Matrices Dinámicos

Declararlo

tipo **NombreDeLaMatriz;

tipo ***NombreDeLaMatriz;

Asignarle un tamaño al Vector(Malloc)

//Genera un array
Matriz = (int **)malloc(filas*sizeof(int *));

//Dentro de cada elemento haz un array
for(i=0; i<filas; i++){
  Matriz[i] = (int*)malloc(columnas*sizeof(int));
}

//Genera un array
Matriz = (int ***)malloc(altura*sizeof(int **));

//Dentro de cada elemento haz un array
for(i=0; i<altura; i++){
  //Genera un array
  Matriz[i] = (int **)malloc(filas*sizeof(int *));

  //Dentro de cada elemento haz un array
  for(j=0; j<filas; j++){
    Matriz[i][j] = (int*)malloc(columnas*sizeof(int));
  }
}

Notación Puntero-Array

Notación
Vector[x];	*(Vector + x);
Vector[x][y];	((Vector+x) + y);
Vector[x][y][z];	((*(Vector+x) + y) + z);

Estructuras

24 diciembre, 20164 enero, 2017Oscar Rosas Deja un comentario

Una estructura es un conjunto de variables que se referencian bajo el mismo nombre. Permite agrupar muchísimas variables de cualquier tipo.

Declaración

typedef struct {
    int algo1;
    char algo2;
    float algo3;
}NombreDeLaEstructura;

La sintaxis de la declaración de una estructura en lenguaje C es:

Forma Correcta

Forma Alterna

struct NombreDeLaEstructura {

int algo1

char algo2

float algo3

}

typedef struct {

int algo1

char algo2

float algo3

} NombreDeLaEstructura

Creación de una instancia de tipo estructura:

NombreDeLaEstructura NombreDeLaInstancia;

Creación de ambos al mismo tiempo:

struct NombreDeLaEstructura {
  int algo1
  char algo2
  float algo3
} NombreDeLaInstancia

Para referenciar un elemento de una estructura se realiza de la siguiente forma:

NombreDeLaInstancia.algo;

Typedef

El lenguaje C permite mediante el uso de la palabra reservada typedef definir nuevos nombres para los tipos de datos existentes, esto no debe confundirse con la creación de un nuevo tipo de datos. La palabra clave typedef permite solo asignarle un nuevo nombre a un tipo de datos ya existente. La sintaxis general de uso de typedef es:

typedef tipo nombre;

Donde tipo es cualquier tipo de datos permitido, y nombre es el nuevo nombre que se desea tenga ese tipo. Veamos algunos ejemplos:

typedef int entero;

typedef struct{
  unsigned código;
  char nombre[40];
  char apellido[40];
}cliente;

Y entonces podrían crearse nuevas variables de la forma:

entero a;

cliente b,*c;

Estructuras y Funciones

Para trabajar con una estructura dentro de una función es muy común usar punteros, que se verían de esta manera:

NombreFuncion(&NombreDeLaInstancia);

donde:

tipo NombreFuncion(*NombreDeLaInstancia){
  NombreDeLaInstancia->algo //Que es igual a: NombreDeLaInstancia.algo
}

Funciones

24 diciembre, 201626 diciembre, 2016Oscar Rosas Deja un comentario

Las funciones son similares a las de cualquier otro lenguaje, pero, tal y como citamos en la introducción, al no ser un lenguaje estructurado por bloques, no es posible declarar funciones dentro de otras funciones.

Son bloques de código que podemos ejecutar una y otra vez.

Sintaxis de la Función:

tipo NombreFuncion(tipo Data1, tipo Data2, ...){
  cuerpo de la función
  return tipo;
}

Donde:

tipo Es un tipo de dato como int o void
Data Es el nombre de una variable

Prototipos

Los prototipos de funciones son una característica de C y se suelen declarar al incio del código.

Un prototipo es una declaración que toma la forma:

Sintaxis del Prototipo:

tipo NombreFuncion(tipo Data1, tipo Data2, ...);

Donde:

tipo Es un tipo de dato como int o void
Data Es el nombre de una variable

Ejemplo:

int fact(int v);
int mayor(int a, int b );
void final();

Argumentos

Los argumentos o parámetros son usados para poder pasar los valores de variables entre funciones.

Si tenemos algo así dentro de main:

...
int x,y;

Funcion(x,y);
...

Entonces el prototipo y la funcion en si podrían ser correspondientemente de estas maneras:

//Prototipo
Tipo Funcion(int x, int y);

//Funcion
Tipo Funcion(int x, int y){
  sentencias
  ...
}

Aunque tambien podrian tener otro nombre los parámetros y funcionaria igual:

//Prototipo
Tipo Funcion(int a, int b);

//Funcion
Tipo Funcion(int a, int b){
  sentencias
  ...
}

Return

Return permite, en primer lugar, salir de la función desde cualquier punto de la misma, y en segundo lugar, devolver un valor del tipo de la función, si ello es necesario (no se devuelve ningún valor si la función es de tipo void).

Paso por Valor y por Referencia

Pasar por Valor

Son cuando se genera una nueva variable dentro de la función, es decir:

Lo que se pasa a la funcion es el valor de X
Las variables que genera la funcion y las originales, son independientes y ningún cambio en ninguna de ellas afecta a la otra.

Funcion(x,y);

Pasar por Referencia

Son cuando se envía la dirección de la variable original a la función, es decir:

Se proporciona a la función una referencia, la dirección de X.
Las variables que genera la funcion y las originales, son dependientes y todo cambio afecta a la otra.

Funcion(&amp;x,&amp;y);

Aquí estaría la función:

tipo Funcion(int *a, int *b){
  sentencias
  ...
}

Recuerda que al hacer usar punteros ya no es necesario usar el & en funciones como scanf:

int funcion(int *vector){
     int i;
     for(i=0; i<n ;i++){
      scanf(“%i”, (vec+i))
     }
}

A diferencia de otros lenguaje, el lenguaje C, sólo permite pasar parámetros a las funciones por valor. Si se desea que los cambios efectuados en una función sobre una variable afecten fuera del alcance de la función, es posible simular un paso por referencia mediante el uso de punteros.

En efecto, si a una función le pasamos como argumento la dirección de una variable, cualquier modificación que se realice en esa dirección, afectará, lógicamente, al valor que tiene la variable original, y con ello, conseguiremos el mismo efecto que un paso por referencia.

Ejemplo:

void Alfa(int *val,float pos){
*val=5;
pos=7.7;
}

void Beta(int val,float *pos){
val=10;
*pos=14.7;
}

int main(void){
int a=6;
float b=9.87;
printf(“Al principio valen a=%d b=%f\n”,a,b);
Alfa(&a,b);

printf(“Después de Alfa valen a=%d b=%f\n”,a,b);
Beta(a,&b);

printf(“Después de Beta valen a=%d b=%f\n”,a,b);
}

Este programa mostrará en pantalla:

Al principio valen a=6 b=9.87
Después de Alfa valen a=5 b=9.87
Después de Beta valen a=5 b=14.7

Ello es, pues a Alfa se le pasa la variable a por «referencia» (se le pasa &a, o sea, un puntero a la variable a), y la variable b por valor, mientras que en Beta sucede al revés.

Arrays y Funciones

Un aspecto a tener muy en cuenta es que C no permite el paso de un array por valor a una función, un array es siempre pasado por «referencia», pues en la llamada, lo que se pasa es la dirección del primer elemento del array (recuérdese que el nombre de un array es un puntero al primer elemento). Por valor tan solo es posible pasar por valor elementos individuales del array, pero no el array completo.

Recursividad

Una función de C puede llamarse a sí misma. Este proceso recibe el nombre de recursividad. Los ejemplos de recursividad abundan, siendo uno de los más habituales la función factorial:

unsigned Factorial(unsigned num){
if (num==0) return 1;
return num*Factorial(num-1);
}

La recursividad es una poderosa herramienta de programación, sin embargo, presenta dos problemas:

La velocidad de ejecución de un algoritmo programado de forma recursiva es mucho más lento que el programado de forma iterativa.
La recursividad, si es excesiva, puede ocasionar el desbordamiento de la pila, y con ello, el fallo en la ejecución del programa.

Punteros

24 diciembre, 20164 enero, 2017Oscar Rosas Deja un comentario

Punteros, punteros, punteros, el tema más difícil de C, pero ya no más.

Vamos a ver en esta lección todo lo relacionado a ellos para que todo sea más fácil para ti en el futuro, así que … Comenzamos

Cada variable tiene un espacio en la memoria RAM. Los punteros son una de las poderosas herramientas que ofrece el lenguaje C a los programadores.

Sin embargo, son también una de las más peligrosas, el uso de punteros sin inicializar es una fuente frecuente de errores en los programas de C, y además, suele producir fallos muy difíciles de localizar y depurar.

Podemos distinguir entre 2 tipos:

Parámetro de Indirección

*←X

Un puntero es una variable que contiene una dirección de memoria
Un Puntero regresa el valor de una dirección de una variable.

Por lo cual se suele decir que el puntero “apunta” a la otra variable.

La sintaxis de la declaración de una variable puntero es:

tipo *nombreDelPuntero;

Donde tipo puede ser int, float,char, ect…

Parámetro de Dirección

&→x

Un parámetro de dirección regresa la dirección de la variable a la que apuntamos.

Cuando usamos el símbolo estamos asignando o refiriendo a una dirección, es decir cuando escribimos &X estamos diciendo la dirección de X.

Es decir el operador & devuelve la dirección de una variable de memoria.

Crear un Puntero

int *puntero;

Asignar a un puntero una dirección de memoria

nombrePuntero = &variableParaApuntar;

Que un puntero regrese el valor al que apunta

variable = *nombrePuntero;

Ejemplos:

int *a
int b,c;

//Si hacemos:
b=15;
a=&amp;b;
c=*a;

Entonces c contendrá el valor 15
Pues *a devuelve el valor de la dirección que sigue (a la que “apunta” la variable puntero), y con anterioridad hemos hecho que a contenga la dirección de memoria de la variable b usando para ello el operador &.

int *a
int b;

//Y hacemos:
a = &amp;b;

La variable puntero a contendrá la dirección de memoria de la variable b.

Operaciones con Punteros

Asignación de Punteros

Es posible asignar el valor de una variable de tipo puntero a otra variable de tipo puntero.Por ejemplo:

int *a,*b
int c;
a=&amp;c;
b=a;

Entonces b contiene el valor de a, y por ello, b también “apunta” a la variable c.

Aritmética de Punteros

Sobre las variables de tipo puntero es posible utilizar los operadores +, -, ++ y —

Estos operadores incrementan o decrementan la posición de memoria a la que “apunta” la variable puntero. El incremento o decremento se realiza de acuerdo al tipo base de la variable de tipo puntero, de ahí la importancia del tipo del que se declara la variable puntero.

Comparaciones de Punteros

Sobre las variables de tipo puntero es posible realizar operaciones de comparación entre ellas. Veamos un ejemplo:

int *a,*b;
if (a&lt;b) printf(“a apunta a una dirección más baja que b”);

Arrays como Punteros

Otra manera de acceder a una parte contigua de la memoria, en lugar de con un arreglo, es con un puntero.

Ya que estamos hablando acerca de las cadenas, las cuales se componen de caracteres, estaremos usando punteros a caracteres, o más bien:

char *string;

Después hacemos que apunte a la dirección de memoria del array

string = &amp;(array[0]);

Ahora estas sentencias son iguales:

array[7];

*(string+7);

Existe una estrecha relación entre los punteros y los arrays. Consideremos el siguiente fragmento de código:

char str[80],*p;

p=str;

int str[80],*p;

p=&str[4];

Este fragmento de código pone en la variable puntero p la dirección del primer elemento del array str. Entonces, es posible acceder al valor de la quinta posición del array mediante str[4] y *(p+4) (recuérdese que los índices de los arrays empiezan en 0).

Esta estrecha relación entre los arrays y los punteros queda más evidente si se tiene en cuenta que el nombre del array sin índice es la dirección de comienzo del array, y, si además, se tiene en cuenta que un puntero puede indexarse como un array unidimensional, por lo cual, en el ejemplo anterior, podríamos referenciar ese elemento como p[4].

Notación
Vector[x];	*(Vector + x);
Vector[x][y];	((Vector+x) + y);
Vector[x][y][z];	((*(Vector+x) + y) + z);

Sin embargo, los punteros sólo tienen una dirección, no pueden contener todos los caracteres de una matriz de caracteres. Esto significa que cuando usamos un char * para realizar un seguimiento de una cadena, debe existir el arreglo de caracteres que contiene la cadena.

Principio de Inducción Matemática

¿Cómo usamos la inducción?

¿…Cómo?

¿Porqué funciona?

Ejemplo #1

Problema para el lector

Ejemplo #2

Ejemplo #3

Compartir es bien:

Congruencias

Clases Congruencia Módulo n

Congruencia Módulo n

Aritmética Modular

Reglas Generales

Operaciones

Función de Euler

Teorema de Euler

Pequeño teorema de Fermat

Teorema Chino del residuo

Problemas diversos

Grupos Permutación

Compartir es bien:

Definición

Dominio y Contradominio

Dominio

Imagen – Contradominio

Relación Inversa

Reflexiva y Irreflexiva

Relación Reflexiva

Relación Irreflexiva

Relación Identidad

Simetría y Antisimetría

Simetría

Antisimetría

Transitividad

Funciones

Tipos de Funciones

Funciones Inyectivas

Funciones Suprayectiva

Funciones Biyectiva

Compartir es bien:

Naturales

Divisibilidad

Algoritmo de la división

Números primos

Máximo Común Divisor

Algoritmo de Euclides

Identidad de Bézout

Algoritmo extendido de Euclides

Ecuaciones diofánticas

Sistemas de numeración

Compartir es bien:

¿Qué son?

¿Cómo Definirlo?

Pertenecia

Forma Básica

Notación Formal

Clasificación de Conjuntos

Conjunto Vacío: φ

Conjunto Universo: U

Subconjuntos A ⊆ B

Operaciones

Intersección

Unión

Resta

Complemento

Diferencia Simétrica

Producto Cartesiano

Ideas Importantes

Tabla

Conjunto Potencia

Ideas Importantes

Tabla

Leyes del Álgebra de Conjuntos

Cardinalidad

Cosas Utiles

Compartir es bien:

Proposiciones

Sentencias Abiertas

Ejemplo:

Función $\varphi$ de Euler