¿Serie vs Sucesión?
Esto es algo que no sabia pero resulta que en matemáticas cuando hablamos una colección de números estamos hablamos de una sucesión, pero cuando hablamos de sumarlos estamos hablando de una serie.
DEFINICIÓN 1:
Podemos definir una serie como: «La suma desde un n0 (generalmente el 0 ó el 1) hasta aproximarse al infinito».
Esto lo podemos expresar visualmente como:
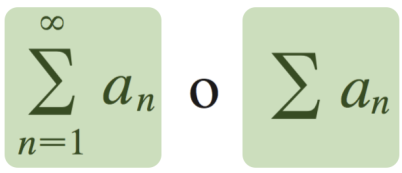
Generalmente empieza en uno, pero tendrá sus excepciones
Sumas Parciales
Veamos otra forma de ver a las series, podemos pensar para ayudarlos a encontrarlas en otra sucesión, en una descrita por las «sumas parciales » osea la suma los elementos de una sucesión, ahora podemos hablar de lo que significa una suma parcial, que no es mas que ir sumando poco a poco todos los elementos de una sucesión.

Sucesión Generada por las Sumas Parciales
Las sumas parciales si te das cuenta CREAR OTRO SUCESION, la cual podemos como a cualquier otra sucesión buscar describir que es lo que pasa cuando se aproxima al infinito, al n-ésimo termino:
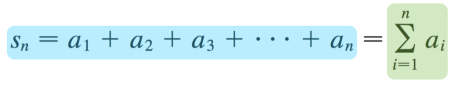
Sumas Parciales
Encontrar la Serie usando Sumas Parciales
Ahora veamos algo, algo muy MUY importante, estas dos cosas son SIEMPRE IGUALES:
- El límite en el infinito de la Sucesión de Sumas Parciales de cierta Sucesión
- La Serie de esa Sucesión
Es decir mas claramente si encontramos el limite de la sucesión de las sumas parciales (llamémoslo s) entonces encontramos cuando vale la serie:

Si encontramos el límite de la sucesión de las sumas parciales
Donde S es:

Bingo, encontramos lo que queríamos.
Propiedades de las Series
Antes que seguir con más tener que recordar que las Series (siempre y cuando convergen, claro ) son un Operador Lineal, es decir:
- Da lo mismo sacar la serie de cierta sucesión y al final multiplicarlo por un escalar, que multiplicar el escalar por cada elemento.
- Da lo mismo sacar la serie de la suma de dos sucesiones que sumar la serie de cada uno de las series.
Esto lo podemos ver mas bonito así:
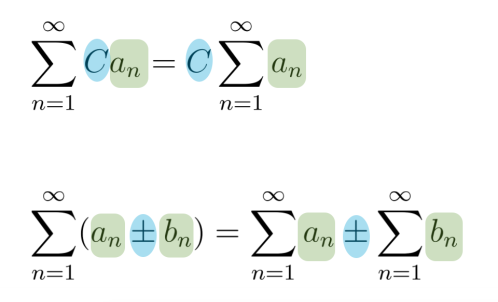
Es un Lindo Operador Lineal (siempre que converge)
Tipos de Series
Hay tantos tipos de Series que después de cierto tiempo empiezas a encontrar muchos patrones, veámoslos y veamos cuanto trabajos podemos ahorrarte ; )
Series Geométricas
Una series se dice que es geométrica si es que si divides dos términos consecutivos siempre obtendrás la MISMA CONSTANTE.
![]()

Ahora podemos ver que la serie de esta sucesión será:

Así se ven
Recuerda: Podemos saber facilmente si converge o no, solo basta con que |r| < 1 para estar seguros de que converge, donde podemos encontrar a que convege también muy fácil como:

Ejemplo:

Series P: La Madre de todas las Armónicas
Para empezar hay que recordar que hay una serie muy famosa que se conoce como la Serie Armónica:

Un clásico
Podemos entonces hablar de las Series P, que es una generalización de las series armo- nicas, de la forma:

Hola P, Soy una Serie P
Recuerda:
- Cuando p ≤ 1 es la serie armónica (La cual diverge).
- Y también podemos saber (por el criterio de la integral) que para cualquiera p > 1 la serie converge.
Series Telescópicas
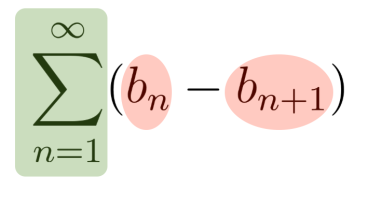
Las series telescópicas son muy lindas, para empezar lo que tenemos que hacer es ver que la Serie (Suma de todos los elementos de la Sucesión) tiene esta forma:

Sumas Parciales
Y si te das cuenta todo eso se cancela, menos dos elementos, por lo podemos escribir así:

Sumas Parciales
Por lo tanto, SOLO CUANDO bn converga ENTONCES LA SERIE CONVERGE a algo entonces podemos concluir que la Suma o Serie es:

Series Alternantes
Son un tipo de serie muy especial en la cual el signo cambia con cada termino. Las lla- mamos como serie alternante porque sus terminos alternan entre positivos y negativos.
Podemos ver aquí que hay dos tipos de Series Alternantes:
- Si empezamos con números positivos es del tipo:

- Si empezamos con números negativos es del tipo:
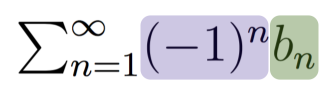
Estimación de Series Alternantes
Una suma parcial de de cualquier serie convergente se puede usar como una aproximación a una suma total, pero no es muy utilizado, a menos que estime la exactitud de la aproximación.
Esto es de verdad muy útil con las Series Alternantes, supongamos una Serie conver- gente. Entonces podemos decir que nuestra estimación será:

Convergencia Absoluta
Decimos que la serie Σan es Absolutamente Convergente si la serie Σ|an|converge.
Si la serie Σan converge pero la serie Σ|an| diverge, decimos que la serie es Condicionalmente Convergente.
Teorema:
Si Σan es absolutamente convergente, entonces también es convergente.
El Teorema anterior es muy útil, ya que garantiza que una serie absolutamente conver- gente es convergente. Sin embargo, su recíproco no es necesariamente cierto: Las series que son Convergentes pueden o no ser Absolutamente Convergentes.
Series de Potencias
Una serie de potencias es una serie donde x es una variable y las cn son constantes que se denominan coeficientes de la serie. Para cada x establecida, la serie ya es una serie de constantes que puede probar para ver si son convergentes o divergentes.

Pero generalmente no es así como lo vemos, sino que tienen esta formula, donde se le conoce como serie de pontencia centrada en a, en (x − a) ó con respecto a a:

Repito, estas series son respecto a «dos variables»:
- x es variable totalmente libre, como una chica francesa.
- cn es un acrónimo para coloca aqui cualquier serie común, como el bn de las alternas.
Radio de Convergencia
Como puedes ver la x en las series de potencias es una incognita que puede valer cualquier número, así decimos que el Radio de Convergencia es el conjunto de todos los valores de x tales que se cumple que dicha serie converge. Ahora veamos como sacar dicho intervalo – conjunto:
- Usa el Criterio de la Razón o de la Raíz como creas mas apropiado y despeja a x de tu resultado, obtendras una desigualdad o algo parecido.
- Ya casi terminas, lo único que te falta es ver que pasa cuando el criterio que elegiste de 1 (pues recuerda que ambos criterios no te dicen nada si L = 1), así que a patita verifica que pasa en ambos límites del intervalo para saber que pasa en ambos extremos (si son cerrados o abiertos).
Obviamente para cualquier Serie de Potencias solo hay 3 posibilidades:
- Solo converge cuando x − a
- La serie converge siempre
- Existe un número R tal que la serie converge si |x − a| < R
Criterios en Series
Pruebas de la Divergencia
Esta es muy clásica y es muy fácil primero hacer esta antes de hacer nada más:

Es decir, que si encuentras que el limite (en el infinito) de la sucesión es 0, puede o no que converge, pero si no es 0, ya ni no intentes xD.
Prueba de la Integral
Suponga que f es una función:
- Continua
- Positiva
- Decreciente en [1, ∞)
y sea an = f(n)
Entonces este criterio nos dira que:

Cuando use la prueba de la integral no es necesario iniciar la serie o la integral en n = 1.
Asimismo, no es necesario que f(x) sea siempre decreciente. Lo importante es que f(x) sea decreciente por último, es decir, decreciente para x más grande que algún número N.
Criterio de Comparación: Directa
Supón que an > 0 y que también bn > 0. Osea que ambos terminos siempre seran positivos. Entonces:

Naturalmente, al usar la prueba por comparación es necesario tener alguna serie co- nocida Σbn para los fines de la comparación. La mayor parte de las veces se usan las series:
- Series P
- Series Geométricas
Criterio de Comparación: Límites
Supón que an > 0 y que también bn > 0. Osea que ambos términos siempre serán positivos.
Entonces si:

(Donde obviamente L debe ser positivo y finito)
Si todo esto se cumple entonces alguna de las dos proposiciones deben ser verdad:
- Ambas Σan y Σbn divergen.
- Ambas Σan y Σbn convergen.
Criterio de Comparación: Razón
Sea una Σan una series de términos positivos, tal que:

- L < 1 : La Serie es absolutamente convergente.
- L > 1 ó L = ∞ : La Serie diverge.
- L = 1 : No nos dirá nada (por ejemplo cualquier serie P nos dará 1)
Criterio de Comparación: Alternas
Podemos ver aquí que hay dos tipos de Series Alternantes:
- Si empezamos con números positivos es del tipo:

- Si empezamos con números negativos es del tipo:
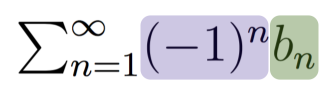
Recuerda que nuestra serie es convergente si cumple con lo siguiente:

Criterio de Comparación: Raíz
Sea una an el n-esímos sumando de una serie, veamos que pasa si hacemos esto:

- laL < 1 : La Serie es absolutamente convergente.
- L > 1 ó L = ∞ : La Serie diverge.
- L = 1 : No nos dirá nada
Ejemplo:

Plan de Acción
- (Prueba de Divergencia) Verifica que el n-ésimo sea 0 cuando n tienda a infinito.
- Verifica si la que tienes es una Serie P ó Geométrica, si si ya sabes que hacer 😉
- (Comparación) Si se pacere a una Serie P o Geométrica, usa alguna de las de Comparación.
- (Convergencia Absoluta) Si quitando que sea alternante se vuelve algo como una P o Geométrica, intenta convergencia absoluta.
- (Criterio de Alternantes) Vea que si es alternante.
- (Razón) Si tienes Factoriales o Potencias, prueba con Razón.
- (Raíz) Si nada funciona, o tienes un termino elevado a la n, intenta la Raíz.
- (Integrales) Si estás re muerto, intenta con Integrales.


