Definición
FORMAS 1:
Se puede considerar que una sucesión es una lista de números escritos en un orden definido:
a1, a2, a3, a4, . . . , an, . . .
FORMA 2:
Es una función en la que su dominio son los enteros positivos, (o los naturales ( pero sin el cero, que algunos ponen el cero ).
Formas de Expresar Sucesiones
Hay dos formas de escribirlas en notación matemática:
Forma de Recursión

Forma General (o aún más pro)

Veamos algunos ejemplos de esta ultima:

Ahora si, vamos a lo que es interesante:
Límite de una Secuencia
El límite de una secuencia (a la que llamaremos {an} ) esta denotado por L (osea que le pondremos de nombre L, pues).

Si el límite existe entonces decimos que la secuencia «converge», sino, decimos que «diverge».
O la definición más formal:

Cortesía de ProfRobBob

ProfRobBob

Ve como esta secuencia se va aproximando en …
Propiedades de los Límites
Hay que recordar que como otros operadores, los limites son operadores lineales, es decir que conservan la suma de elementos y la multiplicación por un escalar:

Esto es un Operador Lineal
Algunas otras propiedades:

Las mas conocidas

Las menos conocidas
Encontrarlo usando Funciones
Podemos ocupar lo que ya sabemos para las funciones con las secuencias para hacer nuestra vida mas sencillas:
Imagine que encuentras una función f(x) tal que:

Donde esta función sea muy especial pues para cada n que se entero se cumple que:

Entonces podemos afirmar de manera muy segura que:

Regla del Gran L’Hôpital’s
Este regla dice que si le estas sacando el límite con respecto a c (donde c puede ser un número cualquiera o bien el infinito o el menos infinito) a una RAZÓN de dos funciones, que si la evaluar de manera directa legas a alguna de estas indeterminaciones:

Límites que son candidatas para Hopital
También se suele decir que para que sea candidato a L’Hôpital’s, la derivada de su denominador debe ser Diferente de cero.
De ser así puedes aplicar el siguiente teorema super bonito (y útil):

(En el caso de que sus derivadas vuelvan a ser una indeterminación como las de arriba, no se te olvide que podemos aplicar esta regla de manera recursiva hasta que nos de algo maldita sea!)
Veamos un ejemplo rápido:

Cotas de una Sucesión
Antes que anda tienes que admitir que este es el teorema con el nombre mas cool.
Antes que nada tenemos que definir que es una cota:
- Una cota inferior es un número que sin importar que n le pongas a tu sucesión, tu cota siempre estará por debajo (o tocando) de la gráfica de tu gráfica.
- Una cota superior es un número que sin importar que n le pongas a tu sucesión, tu cota siempre estará por arriba (o tocando) de la gráfica de tu gráfica.

Diagrama que intenta explicar esto
Ahora podemos decir que esto pasa (Es un teorema):
- Si una sucesión tiene cota superior tiene una mínima cota superior (osea que de todas las cotas posibles dame la mas pequeña, la que casi toca a la secuencia).
- Si una sucesión tiene cota inferior tiene una máxima cota inferior (osea que de todas las cotas posibles dame la mas grande, la que casi toca a la secuencia).
Teorema de Acotación:
Decimos que una secuencia esta acotada cuando tiene una cota superior e inferior.
Sucesiones Monótonas
Veamos dos tipos de secuencias:
Crecientes: Aquellas en las que se cumple esta línea

Decrecientes: Aquellas en las que se cumple esta línea

Una secuencia es monotona cuando es cualquiera de las dos.
Teorema Auxiliar
«Siempre que una sucesión sea monótona y este acotada tiene siempre convergerá a algo»
Teorema del Apachurramiento
El teorema del apachurramiento nos dice los siguiente:
- Supongamos 3 secuencias, a, b, y c tal que:
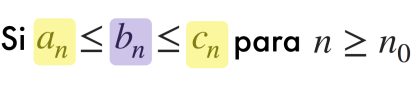
Que cumplan estas características
- Ahora supongamos que:

Encontramos que … 😀
- Entonces podemos concluir que:

Bingo
Teorema Raro
Otro teorema que te puede ayudar es este:
Supongamos que encontremos que:

Entonces si encontramos una f queso ea continua en L, podemos afirmar que:

Veamos un ejemplo:

