Este articulo esta basado en este documento, si quieren ponerse técnicos, tomen palomitas disfruten de muchos, MUCHOS tecnicismos:

Podemos usar las matrices y álgebra lineal para encontrar las soluciones de un sistema de ecuaciones lineales dentro de cualquier campo (eso quiere decir que podemos ocuparla incluso para resolver sistemas en el campo de los complejos o el campo de los números modulo n)

¿Mi sistema se puede resolver? (Prerequsisitos)

Este es muy obvio pero mejor lo digo, TODAS las ecuaciones debe ser lineales, es decir estar escritas de la forma:

Matriz Ampliada

Llamamos a lo que acabo de dibujar una «matriz ampliada» y la podemos notar en dos partes:

---

Tipos de Soluciones

Recordemos antes que nada sobre estas ecuaciones, cada una de ellas representa algo en el espacio y podemos «solucionarlas» al dibujarlas en el espacio:

Y podemos separar nuestras soluciones en 3 amplias zonas:

Sistemas Consistentes

Podemos tener primeramente sistemas consistentes, es decir que tienen mínimo una solución.

Es decir que las 3 rectas se interesectan MÍNIMO en un punto.

Además algo muy interesante es que todo sistema homogéneo, osea que sus coeficientes independientes valgan cero es consistente. Donde la solución mas obvia es que A, B y C valgan CERO.

Así tenemos dos opciones:

• Tocan en un punto: Que es lo «normal» y lo esperado
• Son paralelas.

Este caso es muy especial , pues nos dice que el sistema esta dado por ecuaciones que son múltiplos de la otra o otra forma de verlo es que esta dado por vectores linealmente dependientes, así que de forma numérica cuando tengamos este caso llegamos a algo que siempre es verdad, a una tautología. Te muestro como se ve:

Es decir, ese sistema tiene infinitas soluciones.

Para saber si un sistema es dependiente, por ejemplo si hablamos en dos dimensiones basta con ver que una tiene que ser múltiplo de la otra.

Sistemas No Consistentes

Estos son los feos.

Ocurren cuando llegamos una contradicción, como este estilo:

---

Operaciones Elementales

Para lograr solucionar el sistema se usa lo que se conoce como operaciones elementales, las operaciones elementales son operaciones en las que NO se afectan la solución de la Matriz.

1.- SWAP: Intercambio de Filas / Columnas

Podemos si queremos (aunque no se en que momento quisiéramos) expresar esta operación como una «matriz elemental»

Donde es casi la identidad, pero solo hacemos el swap entre las filas deseadas.

2.-SCALE: Filas / Columnas por un escalar (n no debe ser 0)

Podemos si queremos (aunque no se en que momento quisiéramos) expresar esta operación como una «matriz elemental»

Donde es casi la identidad, pero es k veces la identidad en la fila deseada.

3.- PIVOT: Suma  Filas / Columnas y producto por otra

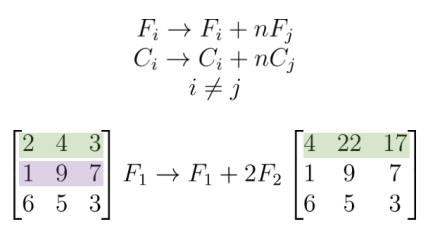
Y a esta también la podemos poder como una matriz elemental, esta es igual que la identidad, pero en la coordenada Y,X (NO x,y) esta el numero que queremos.

Podemos unir las 2 ultimas operaciones y así quedarnos con 2 operaciones:

---

Eliminación Gaussiana

Objetivo: Pasar de una Matriz «normal» a la forma «Escalonada por Filas»

Para ser Escalonada por Filas

Estas no tienen porque ser matrices cuadradas, pero tienen que cumplir con las siguientes características:

• Para toda fila, si existe un elemento distinto de cero (pivote), entonces para todos los elementos anteriores de la fila deben ser cero y este elemento (pivote) debe ser uno.
• Los pivotes deben aparecer de forma escalonada.
• Si una fila no tiene pivotes entonces toda esa fila debe ser nula.
• Si una fila no tiene pivotes (osea que sea nula) entonces todas las de abajo no pueden tener pivotes.

¿Y cómo hago eso? Usando Pivotes.

Pivote: Son los óvalos, se llaman pivotes porque nos vamos a sujetar de ellos y vamos a buscar hacerlos uno y a todo lo demás de esa fila/columna debe buscar hacerse cero.

La Definición Formal: Un pivote es primer elemento de una fila distinto de cero y si o si tiene que ser un uno.

Algoritmo:

1. Inicias en el primer elemento.
2. Convierte ese elemento a uno (usando la operación escalar)
3. Usas ese uno que acabas de crear (usando la operación pivot) para hacer a toda a parte de abajo de la columna sea cero.
4. Te mueves a la siguiente columna y bajas un elemento el columna y repites desde el paso uno.

Código

Soy un estudiante de sistemas computacionales, así que la manera más fácil para mi de entender algo es viendo código, así que te muestro.

---

Gauss Jordan

Objetivo

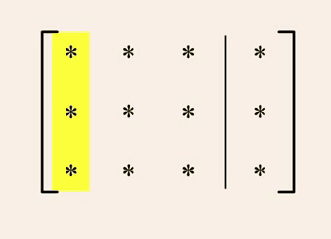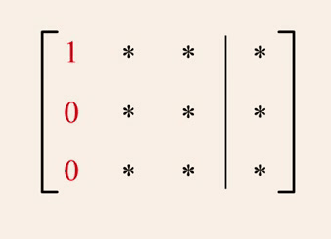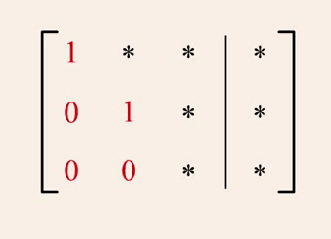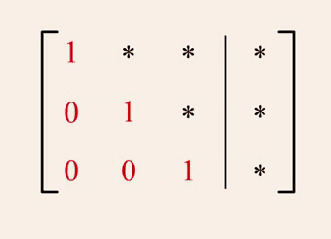
Nuestro objetivo es usando las operaciones elementales encontrar una forma de pasar nuestro matriz ampliada a esta forma:

De una manera más formal es llevar a nuestra matriz a una matriz escalonada reducida:

Decimos que una matriz esta de esta manera cuando ademas de lo arriba, para cualquier pivote toda esa columna (sin contarlo a el mismo) es nulo.

Algoritmo en si:

1. Nos ubicamos en una fila y vemos un elemento
2. Si ese elemento cero:
   1. Entonces encárgate de buscar en los elementos de abajo de esa columna el primer elemento que no sea cero, y cambia la fila y ve al paso 3.1.
   2. Si no encuentras colócate en la siguiente columna de la misma fila en la que estabas y regresa al paso 1.
3. Si no es cero, tenemos nuestro pivote:
   1. Dividir toda la fila entre ese numero para que el elemento sea uno.
   2. Hay que encargarnos de hacer toda esa columna (menos ese elemento) sea cero.
4. Una vez que acabes, colócate en la siguiente fila, en el lugar de la columna en la que estabas mas uno y regresa al paso 1

Código

Soy un estudiante de sistemas computacionales, así que la manera más fácil para mi de entender algo es viendo código, así que te muestro.

---

Tipos de Sistemas

Hay también otra característica de la que ya hemos hablado antes, la dependencia e independencia lineal, un tema bastante difícil, pero también muy importante, y es que las ecuaciones también pueden serlo, veamos:

Sistemas Independientes

Son aquellos que NO contienen ecuaciones dependientes. Y por lo tanto tiene máximo una solución.

Sistemas Dependientes

Son aquellos que SI contienen  (incluso si no son todas) ecuaciones dependientes.

Bajo esta clasificación existen muchos ejemplo erróneos, así que apoyando de imágenes de la Fundación WhyU podemos llegar a ver sus características:

• Un sistema Dependiente  de 2 ecuaciones es fácil de ver, ya que ambas tiene que ser o bien la misma o múltiplos de la misma:

• Un sistema Dependiente  de más de 2 ecuaciones no tiene porque ser múltiplo para ser dependiente, mas bien hay que buscar que una sea una combinación lineal de las otras (o de algunas otras):

• Un sistema Dependiente  NO tiene porque tener soluciones infinitas:

• Un sistema Dependiente  PUEDE no tener solución:

Podemos usar Gauss Jordan para saber si un sistema es dependiente.

---

Ejemplos:

Los mejores ejemplos de estos temas los he encontrado viendo esta serie, de verdad, si saben ingles, vean este video, no se van a arrepentir.