Listas



Tablas

Formularios




Cada página web que visitamos está escrita en un lenguaje llamado HTML. Se puede pensar en HTML como en el esqueleto que le da estructura a la página web.
HTML significa HyperText Markup Language.
Un lenguaje de marcas es un lenguaje de programación utilizado para hacer el texto hacer algo más que sentarse en una página: puede convertir texto en imágenes, enlaces, tablas, listas, y mucho más.
NOTA:
Los códigos HTML tienen a ser muy pesados y largos, así que decidí que todos los códigos de la lección de hoy los pondrán encontrar en GitHub, solo den click, en el menú de arriba.
Es el elemento básico de HTML y se usa en este estilo:
![]()
Etiquetas vacías: Hay algunas etiquetas que no siguen el patrón de arriba, estas se llaman etiquetas vacías y son aquellas en las que no tiene sentido poner nada dentro, como el añadir un salto de línea.
No te preocupes si ahora no tiene sentido, poco a poco iras notando el patrón.
Esta etiqueta es la primera en cada documento de HTML, esta le dice al navegador sepa que se está usando HTML.
![]()

Un archivo en HTML tiene dos partes una cabecera y un cuerpo.
Las partes del Head son muchas y muchas no son totalmente necesarias, así que te dejo un código donde esta comentada cada parte del Head.
| Párrafo | |
| Hipervínculo |
Link de texto  Link de imagen
|
| Imágenes |
| Negrita |
|
| Cursiva |
|
| Subrayado |
| ../ | En la carpeta de arriba |
| ./ | En la carpeta donde estoy |
| / | En la carpeta madre |
![]() Para incluir una nueva línea en un punto y forzar a que el texto que sigue se muestra en la línea inferior, se utiliza la etiqueta.
Para incluir una nueva línea en un punto y forzar a que el texto que sigue se muestra en la línea inferior, se utiliza la etiqueta.
La etiqueta es una de las pocas etiquetas especiales de HTML. La particularidad de
es que es una etiqueta vacía, es decir, no encierra ningún texto. De esta forma, la etiqueta debe abrirse y cerrarse de forma consecutiva:

Dejemos de prestar atención a los lenguajes regulares para una clase mayor de lenguajes, los llamados «lenguajes libre de contexto». Estos lenguajes tienen una notición de manera natural, una notación recursiva.
Se puede decir que es una notación para describir lenguajes.
Es mas poderosa que cualquier autómata finito, pero aun así no puede describir todos los lenguajes.

Diagrama de como Verlos
Es más esto vale la pena verlo, veamos como:
Cada Producción Consta de:

Una variable que esta siendo (parcialmente) definido por la producción, esta variable la llaman de forma común la cabeza de la producción.
Una cadena de cero o mas variables y quizá algunos terminales, el string lo suelen llamar el cuerpo de la producción, que representa una forma de generar los strings, donde simplemente basta con sustituir las variables que estén dentro del cuerpo.

Ejemplo
Veamos un ejemplo de estos lenguajes de esta manera:
Hay varias formas estándar de trabajar estos lenguajes, esta notación es muy muy común en programación, es conocida como Backus-Naur Form así que veámosla:
Usando esta notación nos permite hacer cosas como esta, Naturales:
Podemos pensar en los Autómatas PushDown de la siguiente manera:

Un Dibujito nunca esta de más
Así con cada simbolo que va leyendo el autómata puede hacer 2 acciones:
De manera totalmente formal podemos definir cualquiera de los PDA como:
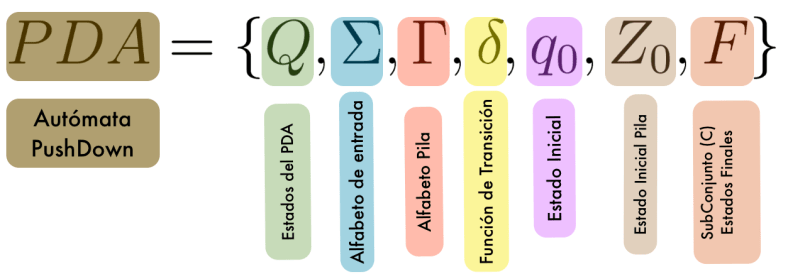
Definición Formal
¿Parece bastante sencillo verdad?
Pues la verdad es que no es tan complejo como tu te podrías imaginar.
Podemos describir el «estado» en cada momento con toda la información del autómata con 3 cosas:
Ahora vamos a centrar nuetra atención a lo que llamaremos una expresión regular, esta sirve como una descripcion algebraica de un lenguaje, de un lenguaje regular, la gran ventaja de trabajar con expresiones regurales en vez de con automatas que es las primeras te permiten ver visulamente (o de forma declarativa) las cadenas que vamos a aceptar.
Antes de nada veamos las operaciones en las expresiones regulares:

Veamos un ejemplo:

La concatenación es el conjunto de todos las cadenas que se crean de concatenar cualquiera de las cadenas de los dos lenguajes.

Veremos un ejemplo:

Recuerda que epsilon es la «identidad» de las concatenaciones, es decir, que calculo la cadena concatenada con epsilon es la misma cadena.

La cerradura es una operacion muy importante, esta te devuelve todos los strigns que pueden ser formados con al hacer la concatenacion de cualquier cantidad de strings de L.
Veamos un ejemplo, así podemos sacar las primeras iteraciones:

Tenemos que saber que no solo hay una forma de expresar las expresiones regulares, por ejemplo, veamos como hacer una RE que sea capaz de recibir cadenas alternantes de 1 y 0.
L = { ε, 0, 1, 101, 10101, 1010101 … 01, 010, 01010 …}

Forma A

Forma B
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | L = { ε, a, b, aa , ab , bb , ba, aaa, …} |
| (a+b)*abb | L = {abb, aabb, babb, aaabb, abad, …} |

Básica

No tan básicas

Las más Hardcore
Para lograr esto vamos a ver varias «ε-NFA» base que nos sirve para encontrar RE más complejas:

Es deir, es imposible que exista tal RE.

Es decir, acepta cualquier RE.

Es decir, acepta cualquier RE que sea la concatenación de R seguido de S.

Es decir, acepta cualquier RE que sea la cerradura de R*.

Es decir, acepta cualquier RE que bien R o S.

Usando esto, como piezas de LEGO, podemos hacer cualquiera RE, veamos todo esto con un ejemplo:
![]()



No haré la explicación pero basado en estos diagramas podemos llegar a :


Recuerda que K no puede ser mas grande que la cantidad de estados:
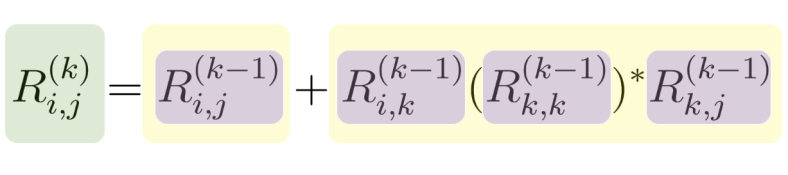
Formula más pro
Espera, espera, ¿Que significa esta «fórmula»?
Para encontrar el Universo de las RE que acepta nuestro autómata tenemos que encontrar los K-Caminos…. Si, esto se explica mejor con un ejemplo…

Nuestro Ejemplo
Nunca olvides que cuando i=j tenemos que añadir el epsilon.
Ahora si, los K-Caminos:
La expresión regular de un autómata es la union de todos los k-caminos en lo que i sea el estado inicial, j es el estado final.
Así en nuestro caso solo importa RE = (1∗0)(0 + 1)∗
Este teorema es tan conocido que ni siquiera quise traducirlo, es demasiado famoso, total, veamos para que sirve el que s considerado el teorema mas importante de las expresiones regulares:
El Pumping Lemma sirve para probar que un lenguaje no es regular, NO ES REGULAR, es decir no nos sirve para probar que sea regular, sino mas bien solo para probar que no es regular.
Digamos que nuestro lenguaje L, es un lenguaje regular, entonces todas las cadenas que pertenezcan a L las podremos dividir en 3 SubStrings usando un numero n (que obviamente tiene que ser menor que la longitud del string original):
Esto es, en español que siempre podremos encontrar una y, no tal lejos del origen que puede ser «repetida o pumped» tantas veces como se quiera (incluso 0 con k=0) y que el string resultante esta aún en L.
La teoría de los autómatas es el estudio de las maquinas «abstractas» de la computación, su objetivo es describir como es que una computadora analiza la información (ignorando la molesta parte física y concentrándonos en la lógica).
Los autómatas son como podemos aplicar las máquinas de Turing en la vida real, son un modelo computacional, es decir, no «son código», son ideas, ideas abstractas que nos permite solucionar problemas.
Un autómata recibe un string, un string de un alfabeto conocido, en general el binario o el ASCII y lo va leyendo un carácter a la vez, nuestro autómata esta hecho de «estados», empezamos en uno (generalmente lo llamamos q0) y dependiendo de que carácter veamos, iremos a otro estado, y así consecutivamente hasta que lleguemos al final de la cadena, cuando llegue este momento, veremos si nuestro estado actual es el final.
Para poder dibujar estos autómatas de manera mas cómoda hemos llegado a un acuerdo sobre cómo podemos dibujarlo.
Todo autómata de estas características, se puede dibujar con las siguientes características:
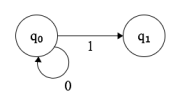
Puedo tener «bucles»
También cada autómata tiene que tener un estado inicial, generalmente a menos que se nos diga otra cosa es el q0:

El autómata siempre empieza en q0
Y también tiene un estado (o más de un uno) que son estados finales, es decir que nos importará cuando termines la cadena, estos son los círculos que tienen un circulo dentro.

El estado inicial también puede ser la final también
Por ejemplo el autómata que ve si la cadena tiene paridad de cero y uno (osea que la cantidad de ceros y la cantidad de unos es par.)

Podemos describir de gran manera como es que se comporta un autómata por su función de transición, esta son las flechas, toma como entrada un estado y un carácter o símbolo y regresa un nuevo estado al que hay que dirigirse.
Hablaremos más de esta función al ver lo tipos de Automátas, pero quería que supieras que existe.
Como vimos, hay dos formas generales de representarlo, ya sea un diagrama o una tabla de estado:


Si nos queremos poner muy formales, vamos a ver como los podemos clasificar:
Aquí la palabra clave es DETERMINISTICO.
Eso quiere decir, que sin importar si lo corremos una vez o mil, si lo hacemos de día o de noche, siempre saldrá el mismo resultado ,es más eso, quiere decir que el azar no entra en ningún lado, que un estado solo puede tener un camino por símbolo.
Repito: Que un estado SOLO puede salir a otro por cada posibilidad. Es decir, que por ejemplo para el estado q3 solo puede haber una flecha que te indique a donde ir si vez un 1.

Además podemos definir el lenguaje de unos de estos autómatas como:
Podemos definir de forma «formal» al lenguaje de uno de estos Automátas como aquel conjunto de strings que cumple con la siguiente expresión:

Es decir, en español: Son todos los string que cuando los pasamos por un autómata finito determinado ( o DFA ) que cuando se le pasan por el autómata, terminan en uno de los estados finales.
Por ejemplo usando algunos autómatas muy comunes algunos Lenguajes Regulares son:
Para poder «analizar» string, usamos una función extra, una que solemos llamar «delta gorro», esta es:

Función
Para analizar este automata:


Aquí la palabra clave es NO DETERMINISTICO.
Son casi iguales que los anteriores, pero hay algo que los hace diferentes y esa única diferencia es la clave, pueden estar varios lugares a la vez.
Esto es porque tiene varios caminos para una misma entrada.
¿Qué?
Pues que basicamente a mi forma de verlo es como la física y la cuántica, cuando nuestro autómata se enfrenta a la decisión, cuando tiene delante dos camino igual de validos, lo que nosotros hacemos es crear dos «universos» uno donde se va por ejemplo por la derecha y otro donde se va a la izquierda, un universo donde va a a q0 y otro donde va a q3 por ejemplo, veamos un diagrama de estas cositas.
¿Qué hace este autómata cuando ve un 0 y esta en q0?



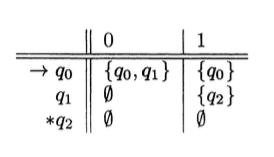
y tiene su tableta también
Es en Delta Gorro donde encontramos las mayores diferencias, pues NO regresa un estado, sino un conjunto, un conjunto de todos los posibles estados, un conjunto de todos los posibles «universos».

Podemos definir de forma «formal» a un lenguaje de un NDA:

Es decir, en español: Son todos los string que cuando los pasamos por un autómata finito NO determinado ( o NFA ) que cuando se le pasan por el autómata, me regresan un conjunto donde AL MENOS uno de sus miembro pertenece a uno de los estados finales.
(O aun más formal: Que entre nuestro conjunto de estados que sale de evaluar w, al hacerle la intersección con el conjunto de los estados finales encontramos que no es nula, es decir, existen estados que estan en nuestro conjunto y que al mismo tiempo son estados finales).
Supongamos el siguiente autómata que se encarga de aceptar cualquier cadena que acabe en 0,1.

Para pasarlo a un Autómata determinada, primero tenemos que hacer una tabla, donde estén: Cada Elemento del Conjunto Potencia, es decir: cada posible subconjunto de todo los estados del autómata, como la siguiente:

Conjunto Potencia
Una vez, listo, podemos hacer una tabla de que pasa a cada subconjunto si ve cada elemento:
Recuerda que la flecha señala al estado inicial y los asteriscos a los estados finales:


(También podemos pasarlo a letras si te es mas cómodo para no escribir tanto)
Ahora lo que hacemos es iniciar por el estado inicial y ver a cuales subconjuntos nos podemos mover hasta llegar al final o a un ciclo.
Gracias a esto podemos dibujarlo:

Diagrama de un Deterministico
¡Y listo!
Ejemplo 2:
Veamos una de mis tareas a ver si deja las cosas más claras:
Añadiremos una nueva característica a nuestro autómata, la que nos permita que lea «nada» literalmente que nos permita no leer nada. Una cadena vacía. Epsilon.
Es más puedes imaginar que nuestra cadena tiene una cantidad necesaria de epsilon dentro de la misma cadena.
Veamos la utilidad en todo esto:
Podemos desarrollar un autómata que se encarga de aceptar decimales, estos consisten en :
Es totalmente posible que una de las dos cadenas este vacía, pero obvio no las dos.
Por ejemplo:

Como siempre, hay que hacer nuestra tabla, pero también hay que contar a epsilon:

En la columna de epsilon va lo que se conoce como la cerradura de epsilon, es decir, es la que nos dice a donde podemos ir solo moviéndonos entre caracteres varios.
Es decir:
![]()
Para poder quitarle los epsilon, tenemos que empezar en q0, mas bien tenemos que empezar en la cerradura de epsilon de cada elemento:

Veamos una de mis tareas a ver si deja las cosas más claras:

A principios del siglo XX los matemáticos estaban fascinados por la pregunta: ¿Cuántas matemáticas podemos hacer? … no usando nuestros sentimientos o intuiciones, sino sólo reglas muy muy cuidadosamente, osea usando un algoritmo.
A final de toda esta cuestión y para que nuestra respuesta tenga algo de sentido tenemos que pensar, ¿Qué entendemos por un programa o algoritmo?

 Y aquí es donde Alan Turing entra en escena con su noción de una máquina de Turing.
Y aquí es donde Alan Turing entra en escena con su noción de una máquina de Turing.
Alan Turing es el hombre que debemos agradecer por un mundo libre de Nazis y lleno de computadoras.
En 1936, Alan Turing publicó un artículo titulado «Computables Numbers, with a Application to the Entscheidungs problem», en el que presentaba la noción de una máquina universal (más tarde llamada «máquina universal de Turing» y luego «máquina de Turing») capaz de computar cualquier cosa que sea computable. El concepto central de la computadora moderna se basó en el papel de Turing.

Propuesta de una máquina de Turing
Deja que te lo explique de otra manera, el en su cabeza pensó en una maquina que pudiera calcular todo aquello que fuera calculable… sin crearla…Antes siquiera de que existiera la primera computadora moderna.
Como podemos leer, Alan es uno de los grandes padres de la computación, y realizo muchísimo trabajos en grandes áreas, así que por ahora nos centraremos en uno de ellos. Su documento «Computables Numbers, with a Application to the Entscheidungs problem»
Como parte de su prueba tenía que trabajar con la noción de cualquier algoritmo posible o cualquier máquina posible. Él tenía que llegar a una forma muy general de como los algoritmos o programas o máquinas trabajan.
Aquí es donde su noción de la máquina de Turing entra. La forma en que Turing describió a estas máquinas es algo como esto:

Tienes una manera de escribir información en forma codificada: Su manera era pensar en una cinta que sea lo largo que sea necesario, esta se divide en cuadrados y cada uno de los cuadrados hay un cero o uno o podemos tener algunos espacios.
Ahora lo que hace nuestra máquina es que mira la cinta un cuadrado a la vez.
Así que se podría imaginado como una pequeña caja corriendo por encima de la cinta, quizás en las ruedas pequeñas, mirando.

Ejemplo de Máquina de Turing

Ejemplo B de la representación de la máquina
Esta cuenta codifica nuestro problema solucionado (una vez que la máquina de Turing haya terminado) lo que una máquina de Turing hace es realmente sencillo:
En cualquier momento en el tiempo está en un estado particular y está mirando un cuadrado en la cinta, y tiene un libro de registro, un libro de programas. Y eso lo dice que hacer.

Computerphile
Si por ejemplo estás en el número de estado 23, Y está mirando un cero, entonces borrar el cero, lo cambia a uno, muévete un cuadrado a la derecha, y pasar al estado número 359.
O si estás en la número 359 y usted está mirando una deje ese uno como es, mueva un cuadrado a la izquierda y pasar al estado número veinte.
Son puras instrucciones sencillas.
Forma B de Entenderlo:

Máquina y su «programa»
Este programa basicamente de dice a la máquina que operación hacer, toda máquina Turing debería tener un inicio, ese esta denotado por:

Estado inicial
Y las operaciones o «instrucciones» más bien tienen esta sintaxis:

Destino e instrucción
Básicamente dice:
Digito1 / Digito 2, Dirección
Ya sabemos que los Dígitos puedes ser: {1,0} y las direcciones: {L(izquierda) , R(derecha) y .(Quédate ahí)}
Así en lenguaje natural la instrucción se lee:
«Si Digito1 es tu dígito actual, continua leyendo, sino para, si continuas leyendo cambia tu estado actual por Digito2 y avanza en Dirección, finalmente estas en el estado q1.»
Si sigues esta idea puedes ver como la máquina va avanzando siguiendo el diagrama:

Diagrama

Primer paso

Segundo paso

Tercer Paso

Cuarto Paso

Paso Final
Esa qh significa Halt, que en español quiere decir «parado» es el paso en el que se dice que se terminaron de ejecutar todas las instrucciones y nuestra máquina a terminado su trabajo y se quedará ahí.
Lo que la máquina hace, es que comienza con un cierto patrón de unos y ceros. Esa sigue estas reglas un cuadrado a la vez, transformando esa cadena de unos y ceros en una cadena diferente de unos y ceros.
Y eventualmente ( y con suerte) la máquina se mueve en un estado de parada.
Está terminado, está hecho. Y lo que queda en la cinta es la respuesta a nuestro problema, codificados como unos y ceros. Eso es un simple proceso, pero resulta que es el esencia de la computación.
Lo que sea cualquier computadora puede hacer, podría en teoría ser hecho por ese sistema mirando a los unos y ceros en una cinta.
Así que por eso decimos que Turing al llegar con su idea de máquinas de Turing, en efecto, surgió un plan para los modernos ordenadores digitales.
Básicamente hacen lo que hacen las máquinas de Turing.
Y usamos esta idea para evaluar la fuerza de los modernos programas de computador. Cuando un programa de computadora puede hacer lo que una máquina de Turing puede hacer, lo llamamos «Turing completa». Y es la cima de la jerarquía de la fuerza del programa.

Así que el programa más fuerte que podemos obtener hace exactamente uno que haga lo que una máquina de Turing puede hacer. Nunca hemos encontrado una forma de calcular más cosas que las que podríamos hacer con una máquina de Turing.
De forma más abstracta podemos decir que una máquina de Turing es como una caja negra, de este estilo:

Máquina Típica de Turing, casual
Así que para evitar tener que desarrollar una nueva máquina para cada operación (lo cual resultaría incontable) se desarrolló la «Máquina Universal de Turing»
Que tenía una entrada P que le diría como tenía que comportarse y esta máquina para el mundo exterior serviría exactamente igual que una máquina de Turing normal, si de esas que te encuentras todos los días.

Hay también un problema muy famoso relacionado con el bueno de Turing y de como en la solución de ese problema, Alan Turing casi inadvertidamente inventó la computadora digital moderna.
Así que empezamos de nuevo al principio del Siglo XX, donde los matemáticos tenían planteado este problema:
En lógica estamos interesado en encontrar la respuesta a la pregunta: «¿Estas premisas implican esta conclusión?
Las premisas son los bits con los que comienzas, son los pedacitos que sabemos en el principio (osea los supuestos) y la conclusión es el a lo que quieres llegar.
Hay una prueba llamada Halting que nos diría si las premisas conducen a las conclusiones por medio de la lógica. Es decir ¿Hay una manera automática de averiguar si lo hacen o si no lo hacen? , así que ese es el problema, se llama el también el Problema de Decisión.

Turing es feliz
Los matemáticos querían saber hay una respuesta al problema de la decisión para la lógica de primer orden (Ese es el tipo de lógica que aprendes en Filosofía o matemáticas en la universidad).
Alan Turing fue uno de los primeros en descubrir que la lógica de primer orden no es decidiste, es decir puede probar automáticamente si las premisas llevan a la conclusión.
Para probar esto es realmente difícil (conceptualmente) porque tenemos que ser capaz de demostrar no hay ningún programa posible que pueda darnos la respuesta.
Pero, ¿cómo lo haces hacemos ¿Cómo se muestra algo de todos los programas posibles que puedan existir?
Turing surgió con una brillante solución, su idea es algo así:

ComputerPhile
Supongamos que tenemos un programa y vamos a dibujar como una caja negra, (una de las maquinas de Turing)
Esta máquina va a tomar unas premisas y conclusiones y te dice que las premisas llevan a la conclusión de manera automática, es decir resulte el problema de Halting.
Ahora aquí hay otra pregunta que podemos hacer, que es equivalente:
¿Alguna vez el programa terminará?
Veamos todos los posibles programas que existen y sólo pensemos en ellos como cajas negras y por el momento lo único que nos interesa saber es si algún día pararan de «correr».
No nos importa que respuesta nos den estos programas, simplemente saber si nos darán una respuesta.
Si no terminara nunca de «ejecutarse» el programa significa que quedo atrapado en un bucle infinito. Nunca sabríamos si va a termina hoy, mañana o nunca.
Lo asombroso resulta en que nuestro problema lógico: ¿Estas premisas implican esta conclusión? es muy similar a este Problema de Detención.
La parte inteligente de la prueba de Turing es que para mostrar que es imposible que existe una máquina, no importa lo compleja que sea que resuelva el problema de la Parada… Pero ¿Cómo lo hizo?
Supongamos que tenemos una máquina o un programa que soluciona el problema, no nos preocupemos de como lo hace, simplemente lo hace.

La vamos a llamar Máquina H
Esta máquina recibe dos entradas, un programa y un «entrada de programa» y nos regresa un «si» si en algún momento el programa P se detendrá dado la entrada I, y un «no» si… si no (obvio).

Máquina H+
Usando H como base podemos crear esta nueva máquina en la que si el resultado es verdadero entonces haremos que se quede en un bucle para siempre y si la respuesta es no, entonces regresamos un «si parará».
La magia ocurre cuando alimentas a H+ con H+

Así que la pregunta que ahora estoy haciendo es que estoy haciendo es preguntarle a la máquina: ¿H + se parará con la entrada H+?
Y aquí es donde todo va mal porque si H+ detiene recibimos una respuesta afirmativa, pero entonces inmediatamente entra en un bucle infinito, y por consiguiente no se detiene.
Por otro lado si recibimos un «no se detiene» de H entonces la máquina nos devuelve un «Si se detiene» y se detiene.
No es que hayas entendido mal, es que es una paradoja, no tiene sentido, pero lo que muestra es que empezamos suponiendo que podemos resolver el problema y hemos terminado con una paradoja, por lo tanto la suposición era mala.

Ahora entiendes este meme
Resulta que no hay máquina posible, ningún programa posible que resuelva el Problema de la Parada.
 |
 |
 |
|
Para empezar con esto, veremos antes ¿Qué es un lenguaje desde un punto de vista completamente matemático?
Para definir un lenguaje (que es la parte fundamental de la teoría de autómatas) tenemos que definir algo más elemental, un alfabeto:

Un alfabeto es finito (y que obviamente no esta vacío, sino no tiene sentido) de forma común usamos el símbolo de suma.
Algunos alfabetos comunes son:

Un string o una palabra es una secuencia finita de símbolos de un alfabeto. Por ejemplo, 01101 es una cadena del alfabeto binario. La cadena 111 es otra cadena de este alfabeto.
Cadena Vacía: Hay una cadena muy especial y que siempre tiene que existir, y es un string sin ningún símbolo.
![]()
A menudo es útil clasificar cadenas por su longitud, es decir, el número de símbolos en la cadena. Por ejemplo, 01101 tiene longitud 5. La notación estándar para la longitud de una cadena:

Si tenemos un alfabeto cualquiera, podemos expresar el conjunto de todas las cadenas de una cierta longitud usando la notación de potencia.
Así elevar un alfabeto a una potencia K es lo mismo que preguntar por todos los posibles strings con longitud K.

De aquí podemos sacar la gran pregunta, ¿Cuál es la diferencia entre el la segunda y la tercera línea? El primero es un alfabeto; sus miembros 0 y 1 son símbolos. El segundo es un conjunto de strings cual longitud son uno.
Así para denotar el conjunto de todos los posible strings usamos:

A veces es útil excluir a la cadena vacía, por lo que tenemos la siguiente notación y propiedades:

Un conjunto de cadenas de todo el universo posible es lo que llamamos un lenguaje. Es decir:

No es necesario incluir todas las cadenas posibles, solo un conjunto de ese conjunto enorme que tenemos para elegir.
La elección del término «lenguaje» puede parecer extraña. Sin embargo, los idiomas se pueden ver como conjuntos de cadenas. Un ejemplo es el inglés, donde la colección de palabras es un conjunto de cadenas sobre el alfabeto que consiste de todas las letras. Otro ejemplo es C, o cualquier otro lenguaje de programación.
Aquí otros ejemplos:
La única restricción importante en lo que puede ser un lenguaje es que todos los alfabetos son finitos. Así aunque un lenguaje puede tener un número infinito de cadenas, solo puede sacarlos de un numero finito de símbolos.